

SUDOKU WHEN YOU GET STUCK: AVOID TRIAL AND ERROR, MASTER SOLVING STRATEGIES
Improve your ability to recognize patterns and you will get better at Sudoku. This is true to any Sudoku player, beginner or expert. With our Sudoku puzzle books, never worry about getting stuck at a certain step. Getting stuck is an opportunity. It is the opportunity to learn and become better at recognizing patterns. The more you get stuck, the stronger you become. And your growth is simply much faster when you have ready access to the solution to the step where you got stuck on. You can review how to get passed that step, acquire a new skill, and continue solving your puzzle on your own. With any book from our collection all the steps of resolution of a puzzle are readily accessible to the player.
Let’s dive straight into the experience of following a guided solution to two fascinating Sudoku puzzles using the most intuitive solving logic.
The human logic is to always start with the simplest solving techniques and gradually use harder ones when the easier ones are exhausted. Most players start a Sudoku by finding hidden singles (easy Sudoku puzzles). Then they move to intermediate strategies mostly consisting of scanning for naked singles in two or three dimensions (medium Sudoku puzzles). Then they step up with hard solving techniques by looking first for naked or hidden pairs, triples or quads, then pointing pairs or pointing triples, then boxed pairs or boxed triples (hard to very hard Sudoku puzzles). Then they shift to expert strategies starting with X-wings, then remote pairs, then XY-chains, and finally swordfish (extreme to diabolical Sudoku puzzles). To teach yourself and master any of these techniques, we have a great tool that challenges you by putting you in situations where you are forced to use the techniques. You can get to the tool by clicking on this link.
We will use the following naming convention for the components of a Sudoku grid: row, column, box, cell.
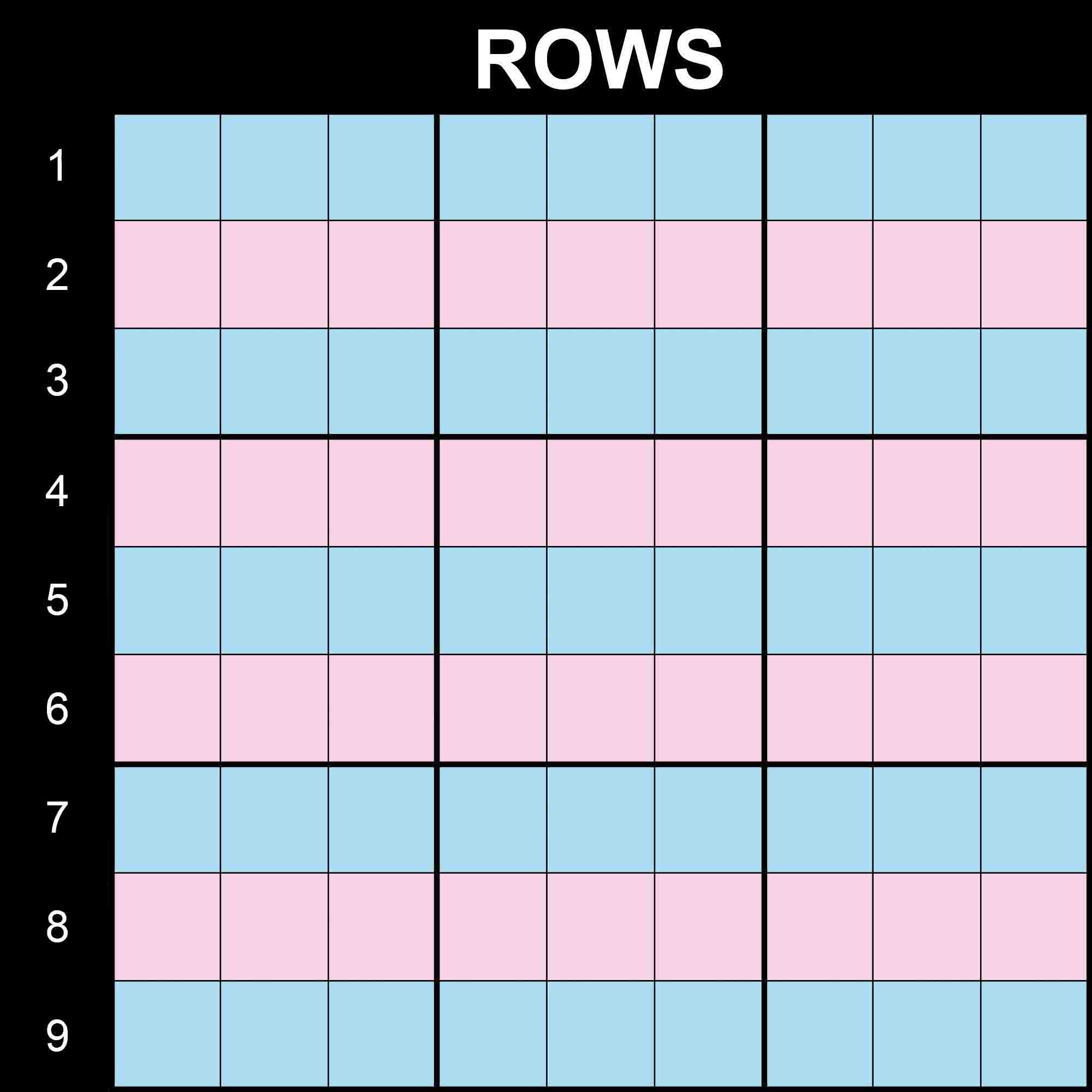
A classic Sudoku puzzle has 9 rows. We will refer to the first row at the top as row 1 and to the last row at the bottom as row 9.

A classic Sudoku puzzle has 9 columns. We will refer to the first column on the left as column 1 and to the last column on the right as column 9.
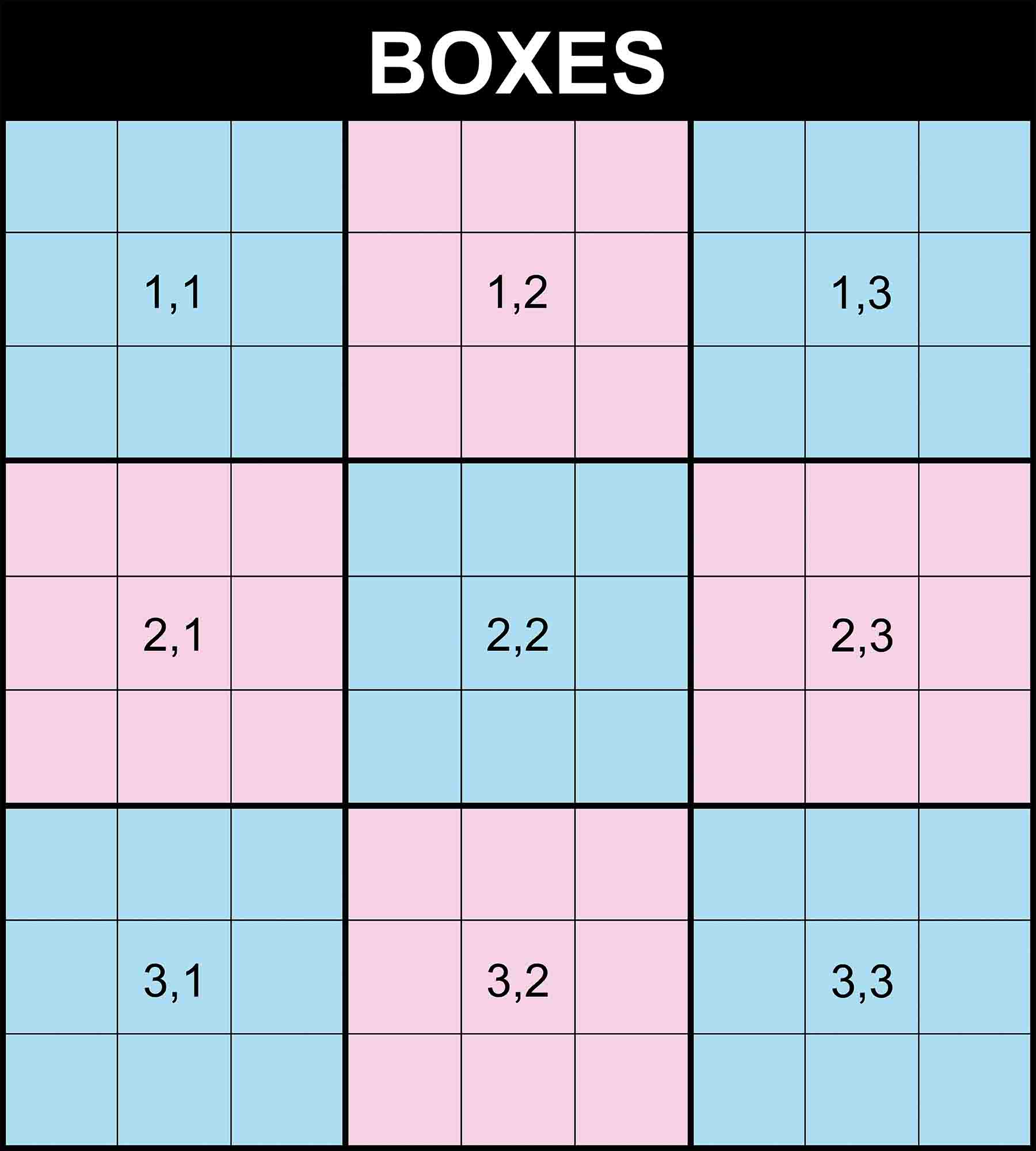
A classic Sudoku puzzle has 9 boxes. We will refer to the first box at the top left as box (1,1) and to the last box at the bottom right as box (3,3).
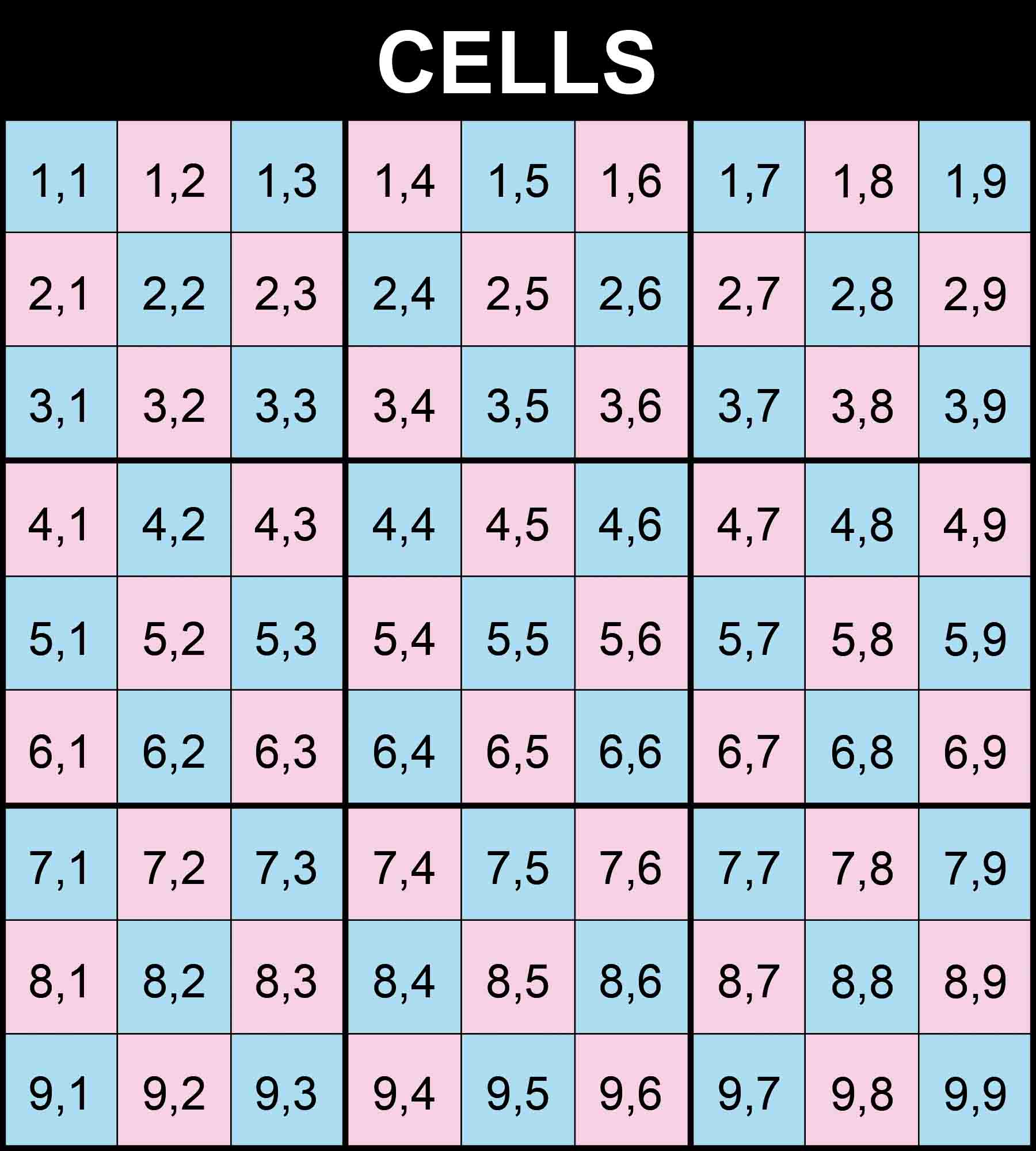
A classic Sudoku puzzle has 81 cells. We will refer to the first cell at the top left as cell (1,1) and to the last cell at the bottom right as cell (9,9).

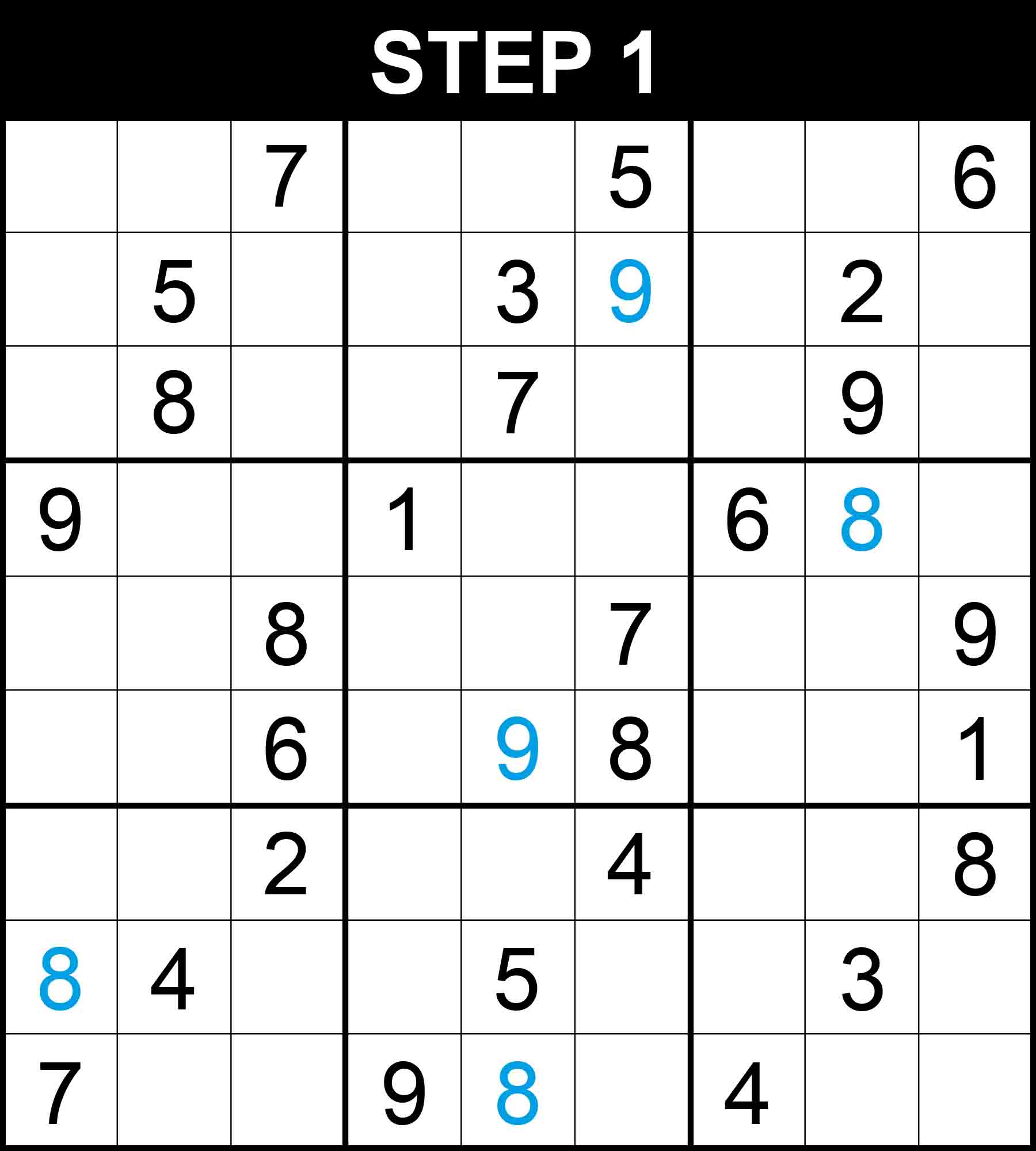
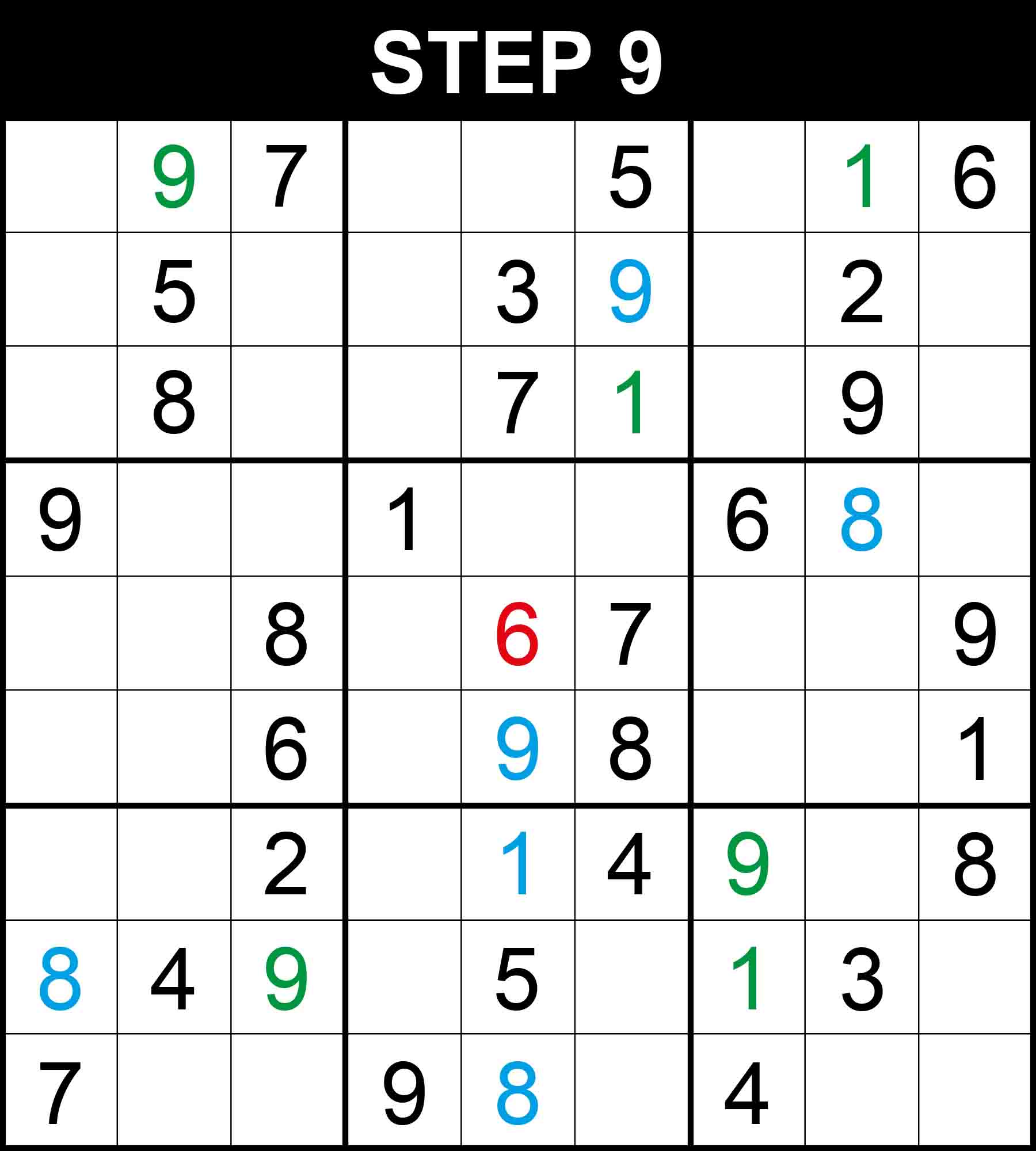
With 29 hints only and 5 hard steps where you may potentially get stuck at, this puzzle can be considered a challenging puzzle. Let’s follow its step-by-step solution in 24 steps. New values found through an easy step are highlighted in green, those found through a medium step are written in blue, and those found through a hard step are presented in red.
Note: This puzzle comes from one of our challenging Sudoku books. It is the first and least challenging Sudoku puzzle in the book Very Hard Sudoku. All 340 puzzles in the book have a readily accessible step-by-step solution. You can get a copy on Amazon and solve 340 challenging puzzles by following this link.
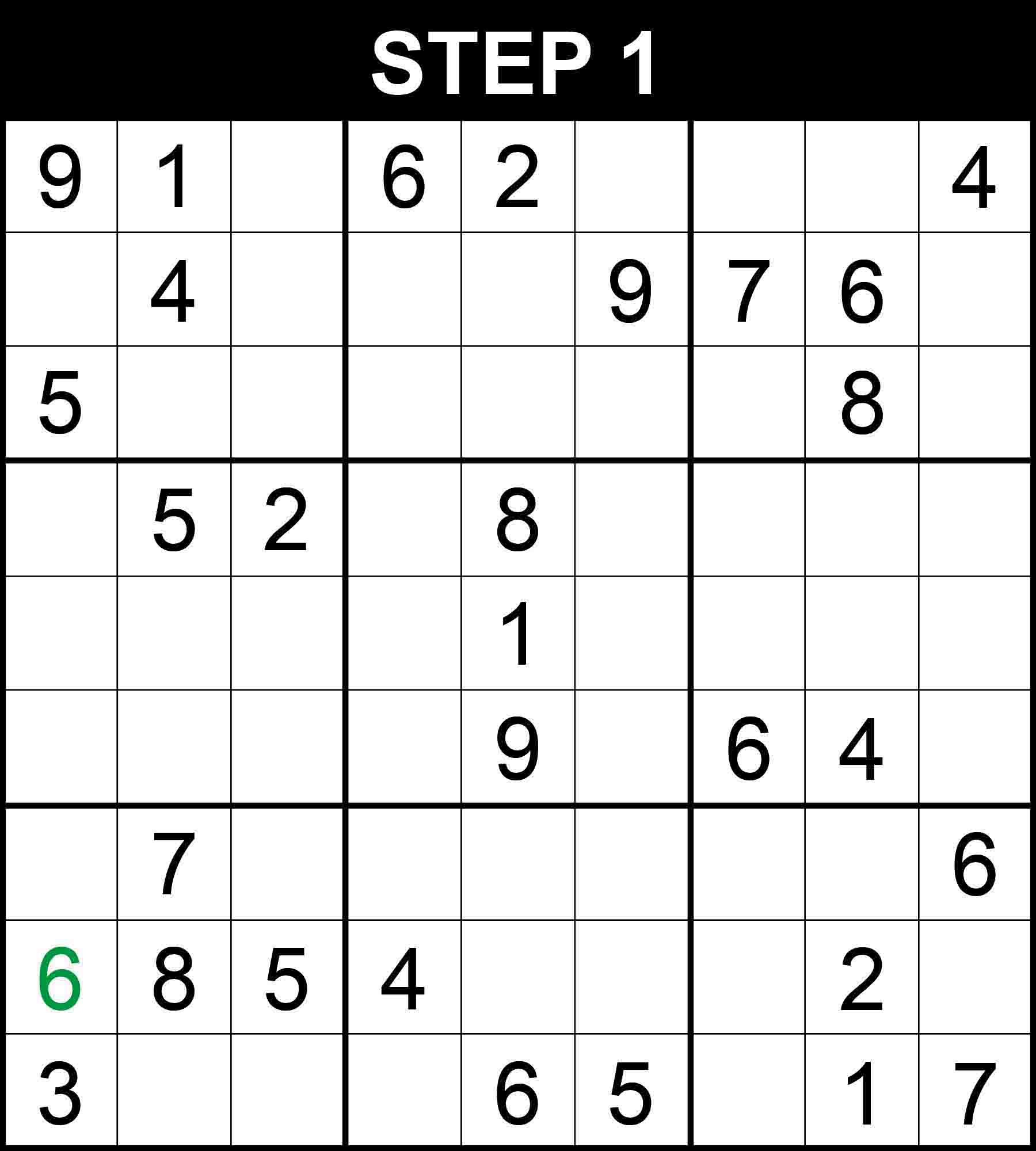
There is a single position for 6 in row 8. The other cells in the row cannot contain 6 because their boxes already contain a 6.
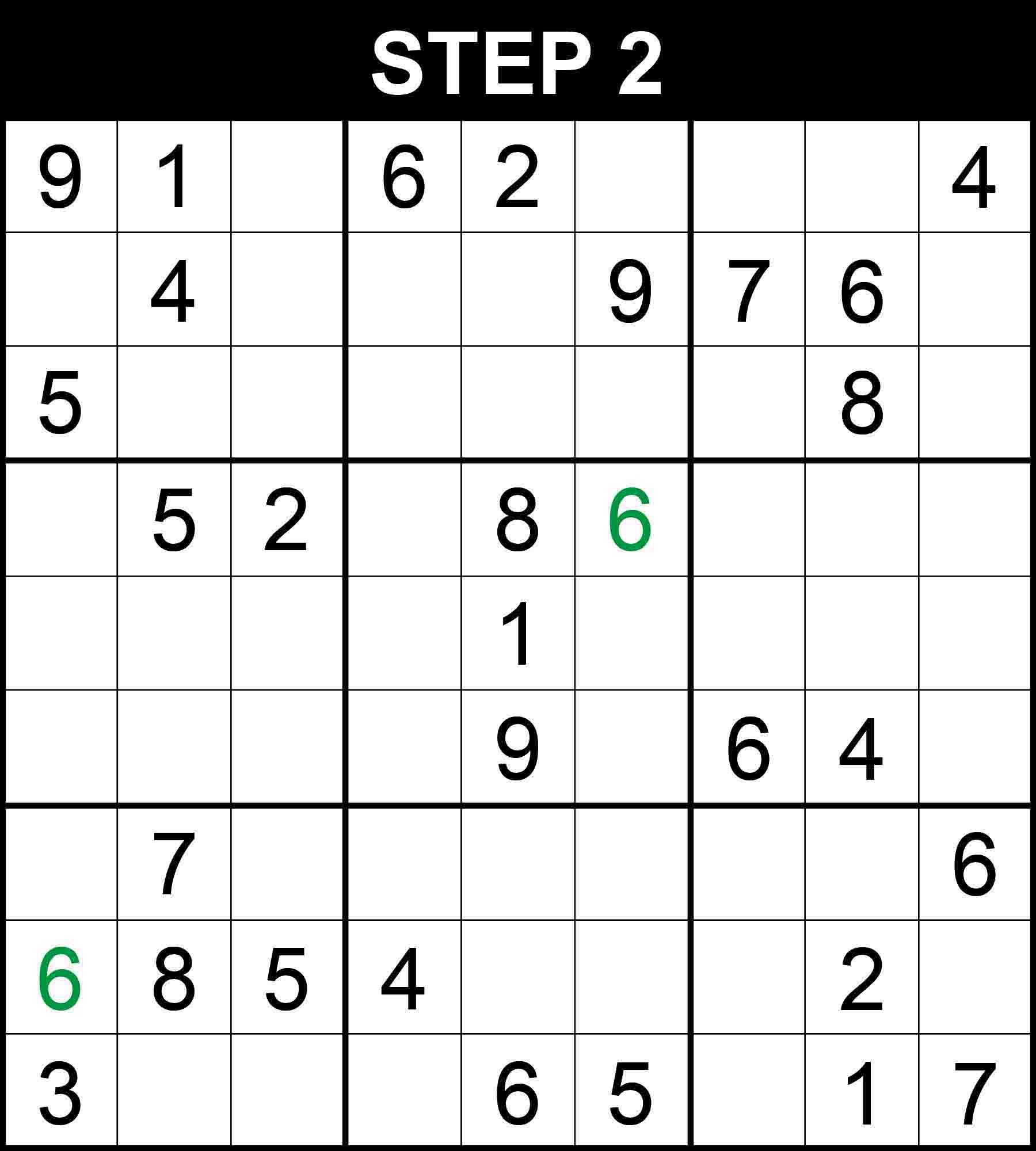
There is a single position for 6 in row 4. The other cells in the row cannot contain 6 because their columns already contain a 6.
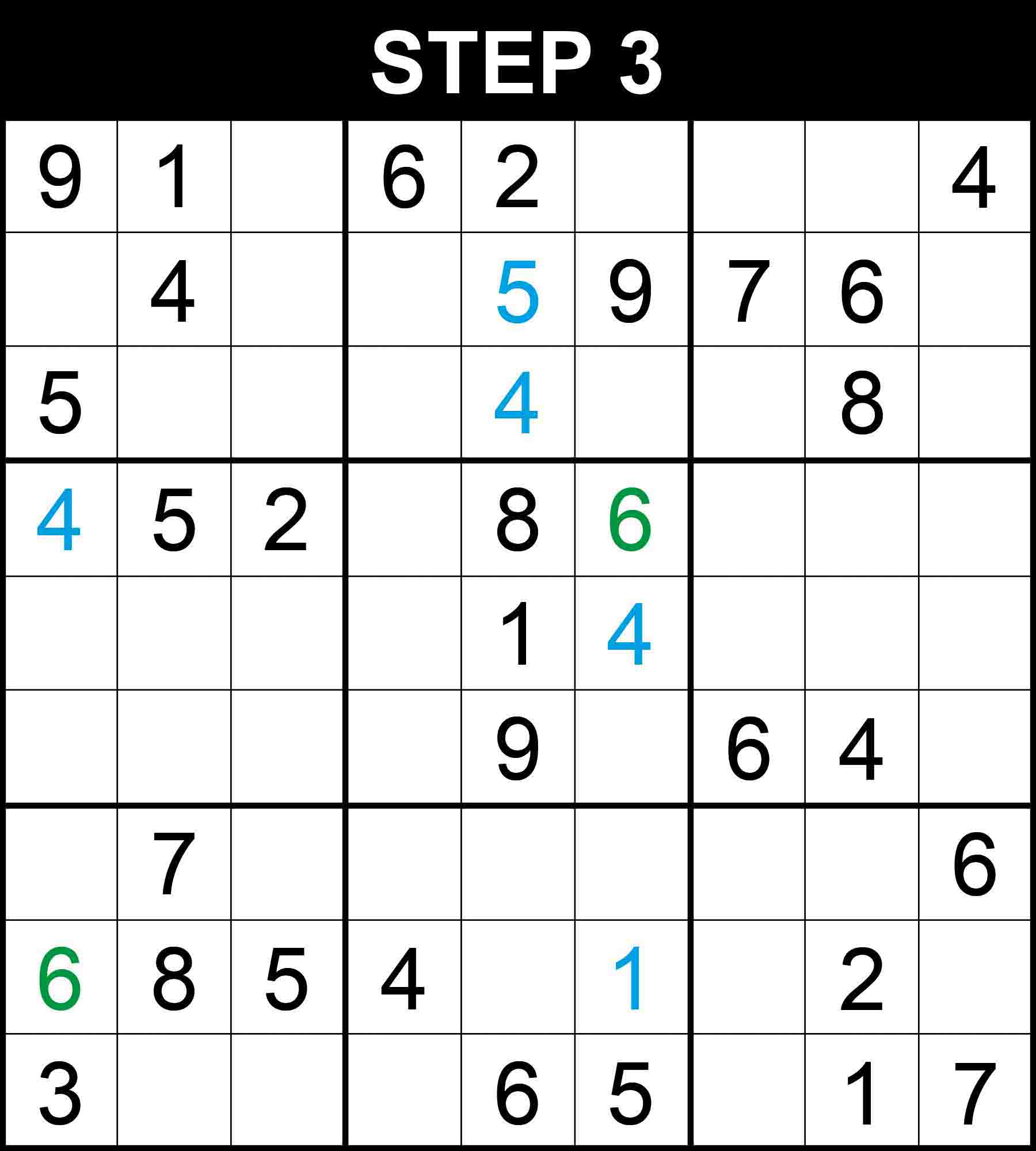
There is a single position for 4 in row 4, 1 in row 8, 4 in column 5, 5 in column 5, 4 in box (2,2). The other cells in these dimensions cannot contain those numbers because their rows, columns, or boxes already contain them.
There is a single position for 7 in row 8. The other cells in the row cannot contain 7 because their columns already contain a 7.
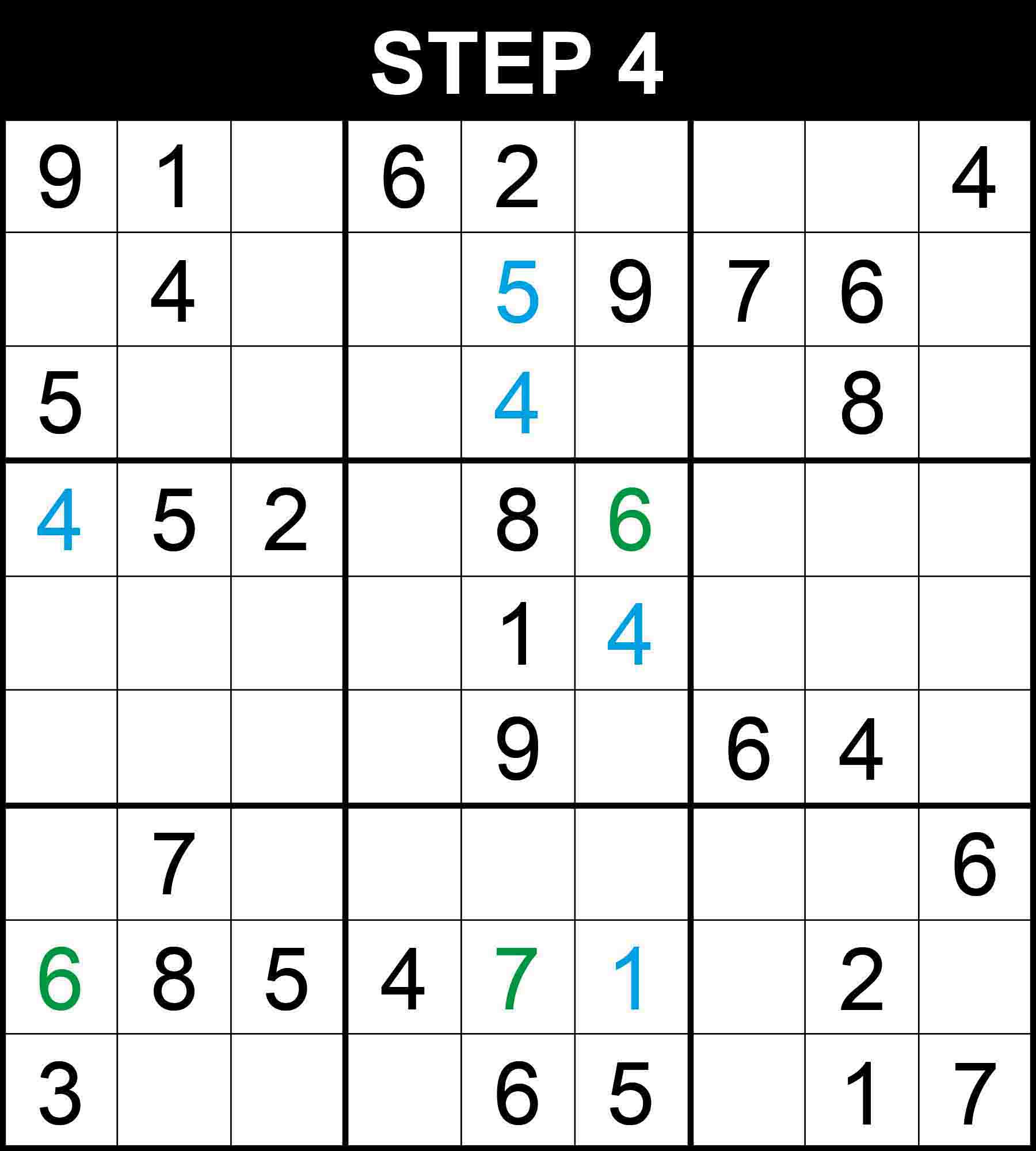
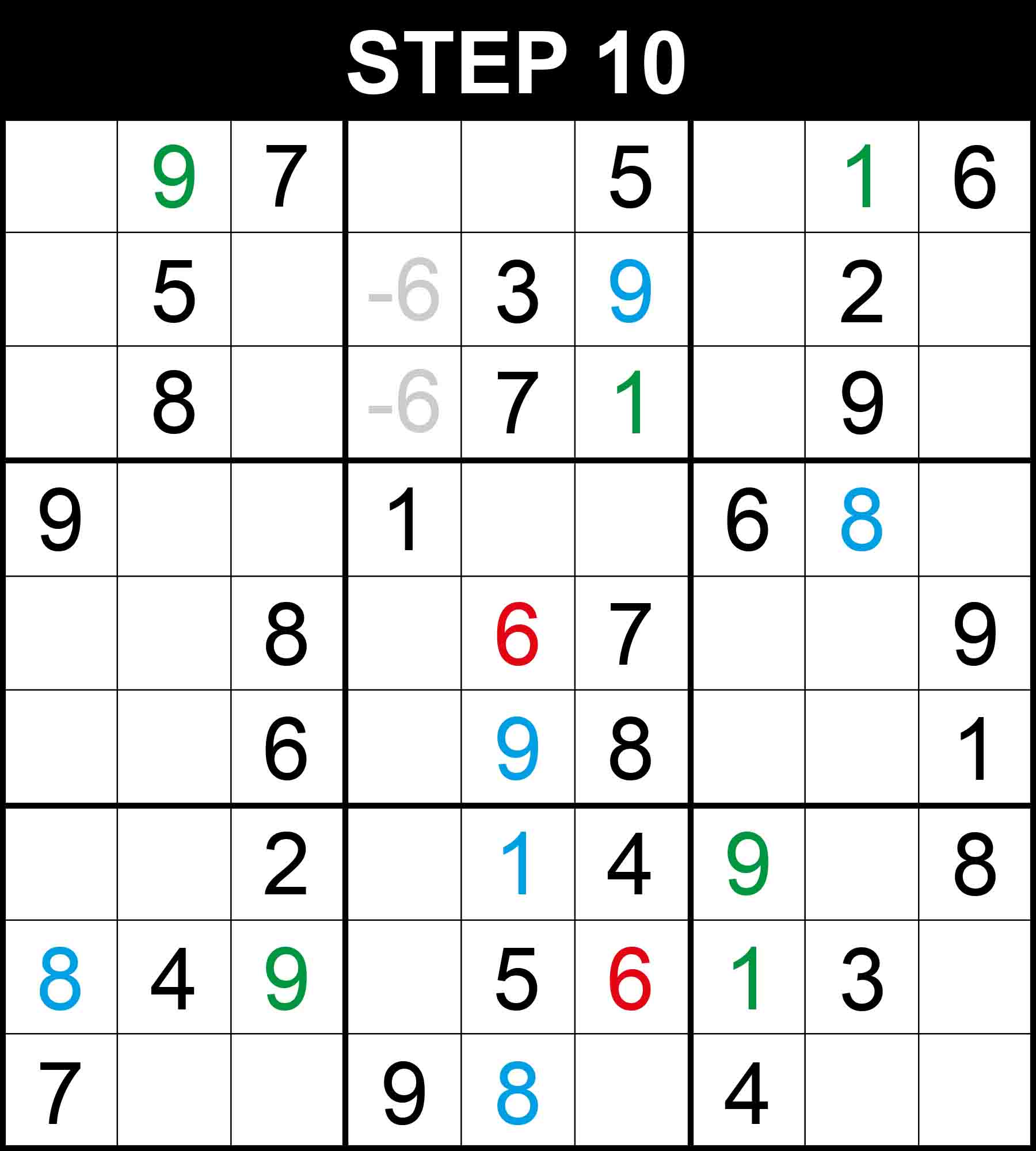
Looking at column 5, 3 is the only missing value at (7,5).
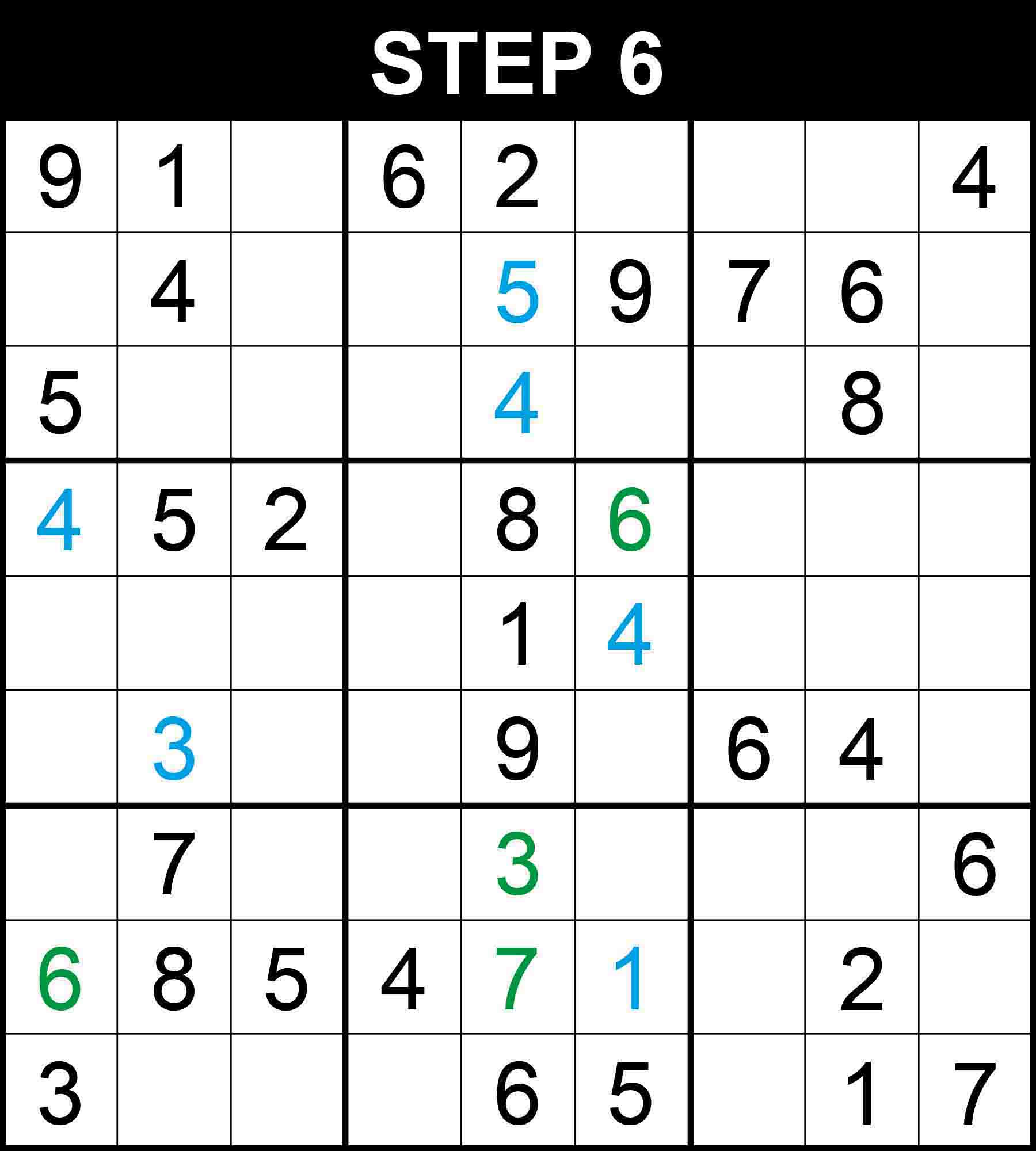
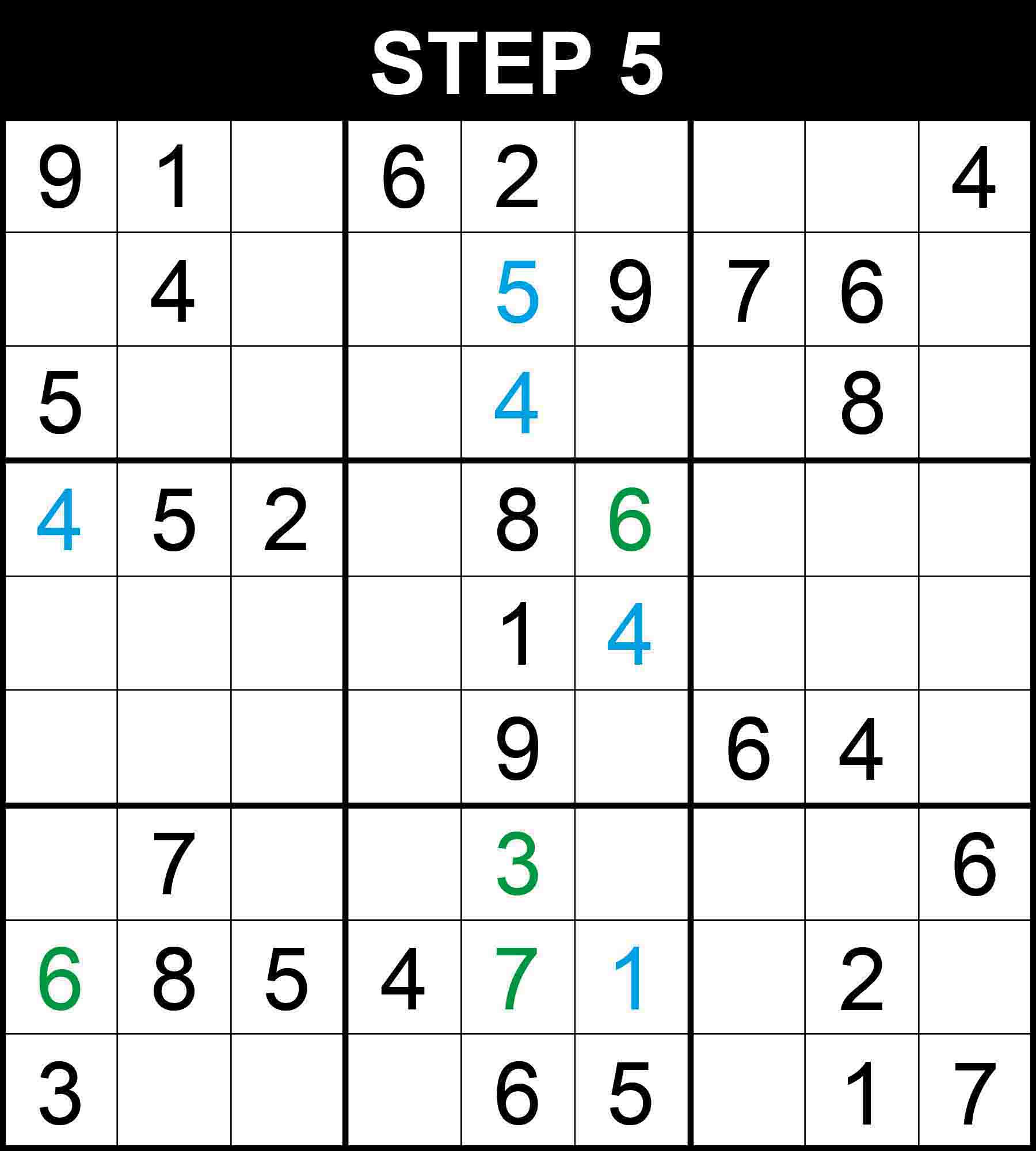
Looking at row 6, column 2 and box (2,1), 3 is the only missing value at (6,2).
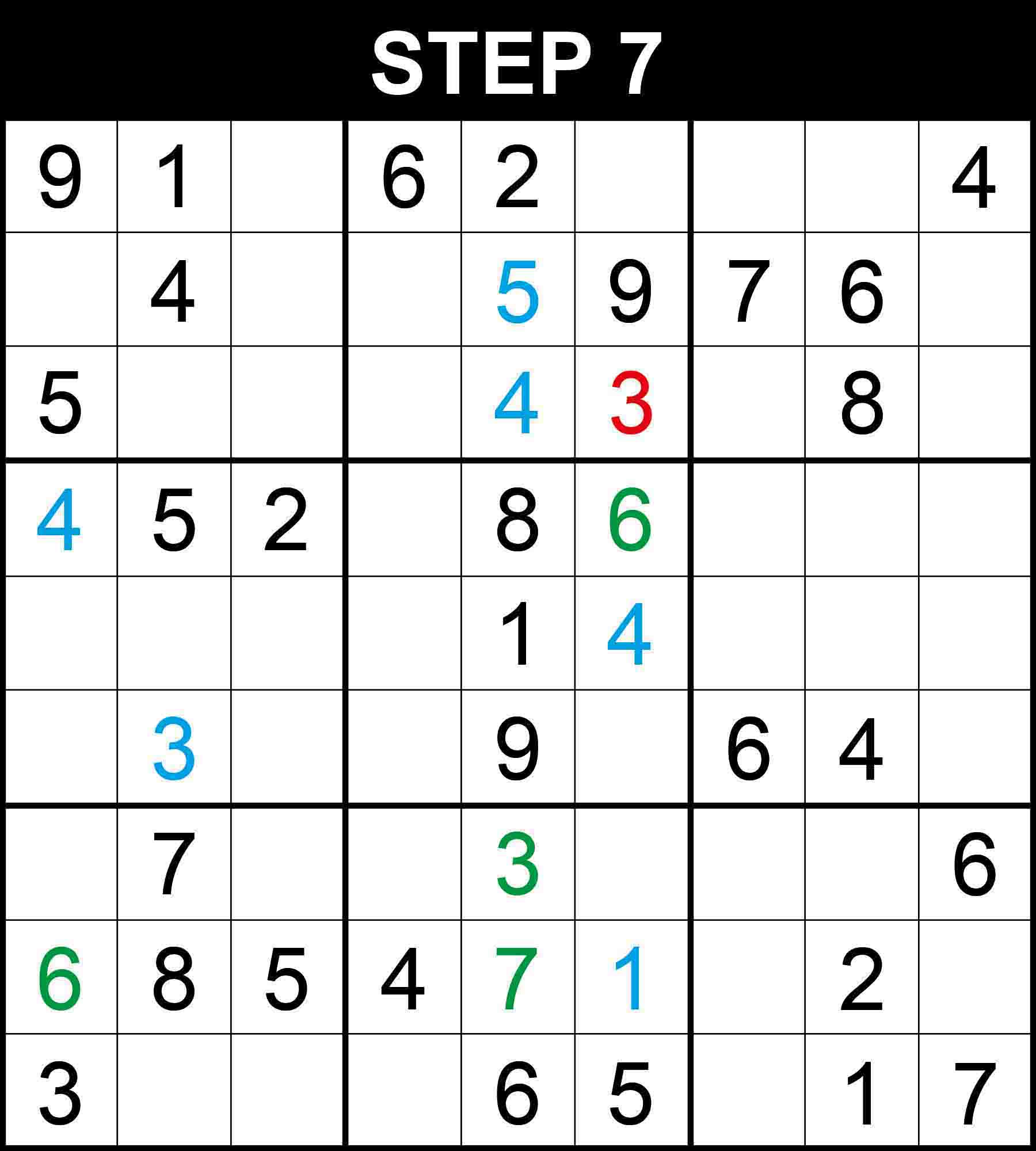
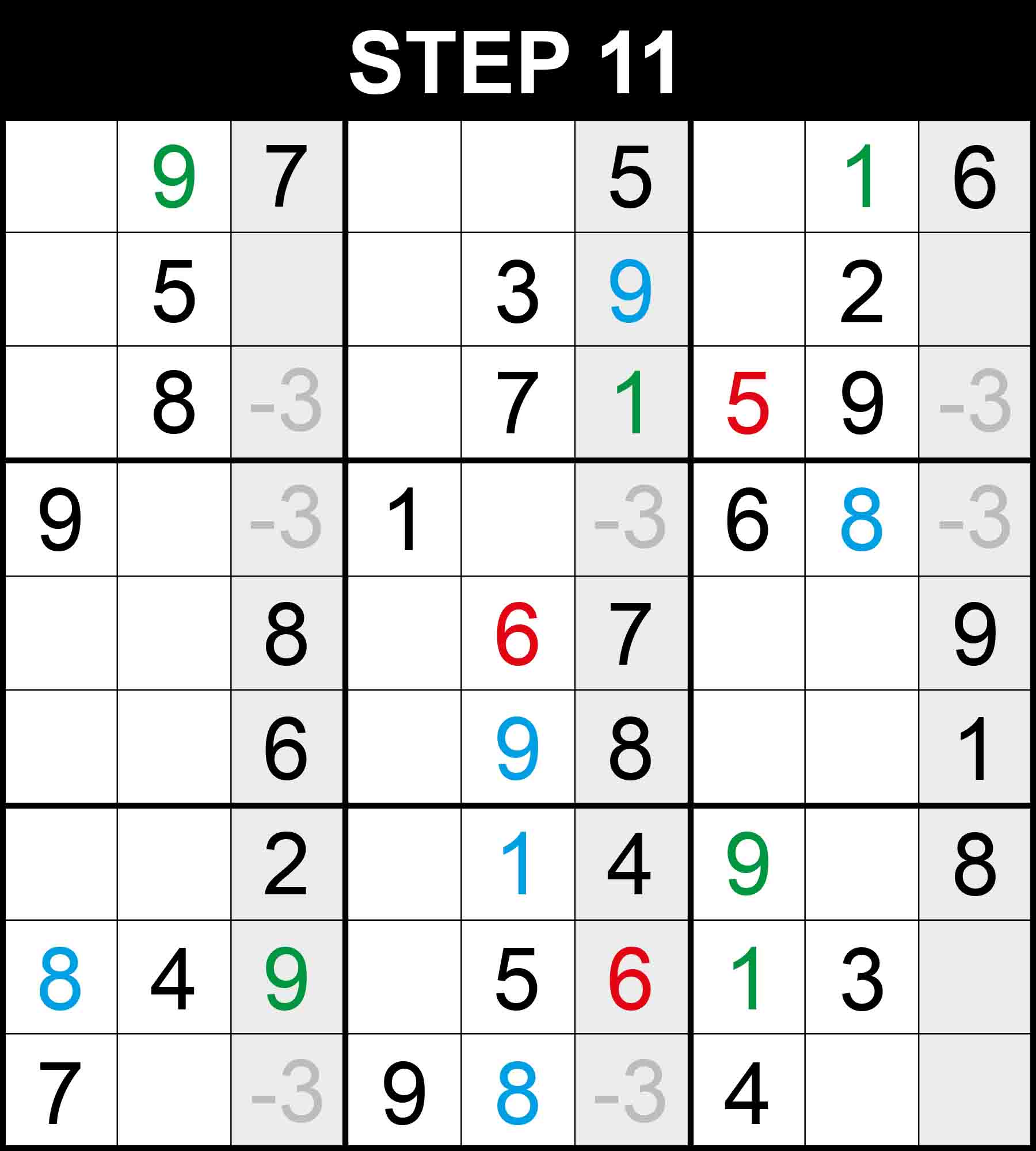
Cells (1,3) and (1,6) are the only positions for the candidates 7 and 8 in row 1 because the other cells in the row cannot contain 7 or 8. Therefore, There is a single position for 3 in column 6.
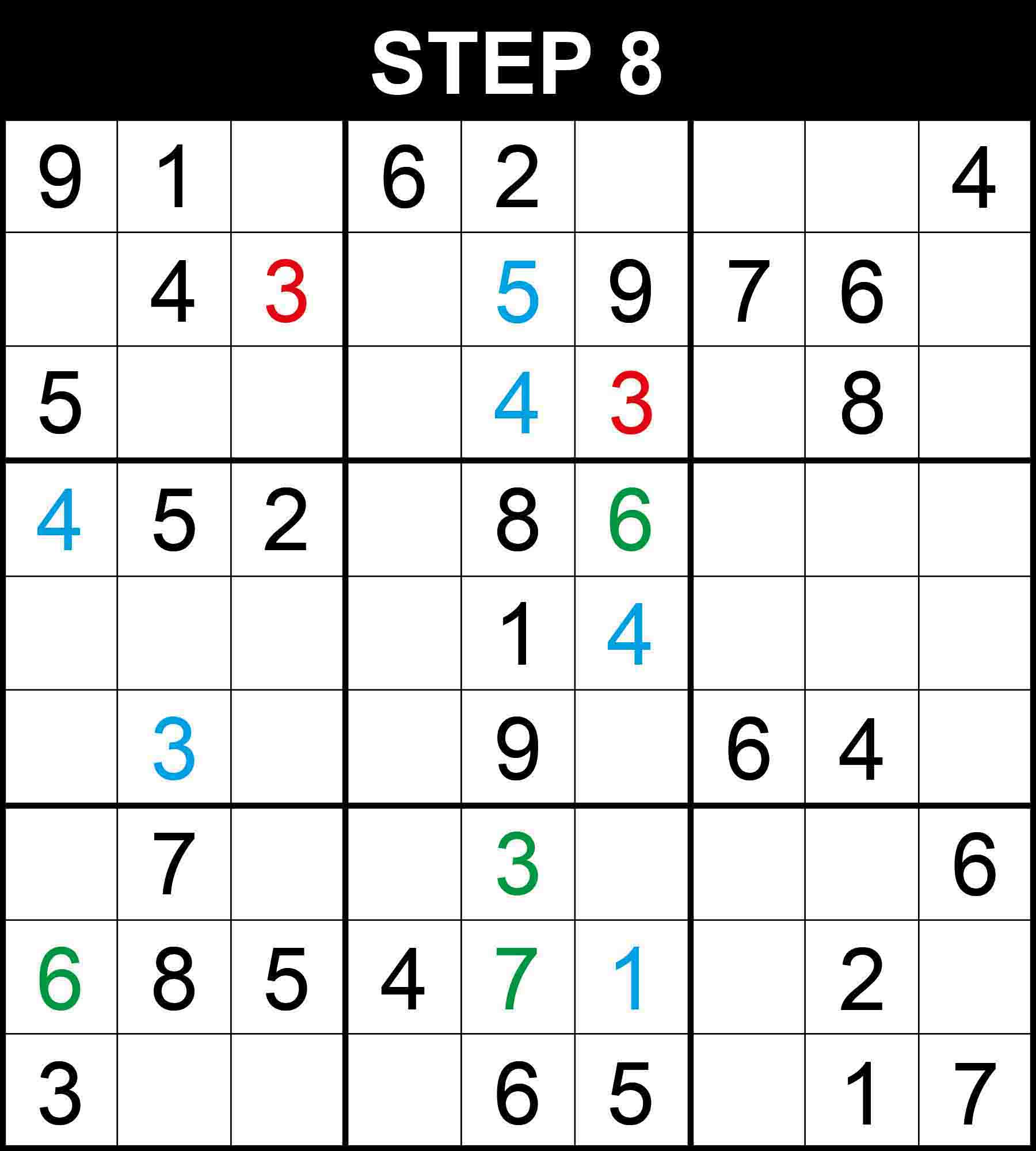
Cells (1,3) and (1,6) are the only positions for the candidates 7 and 8 in row 1 because the other cells in the row cannot contain 7 or 8. Therefore, There is a single position for 3 in column 3.
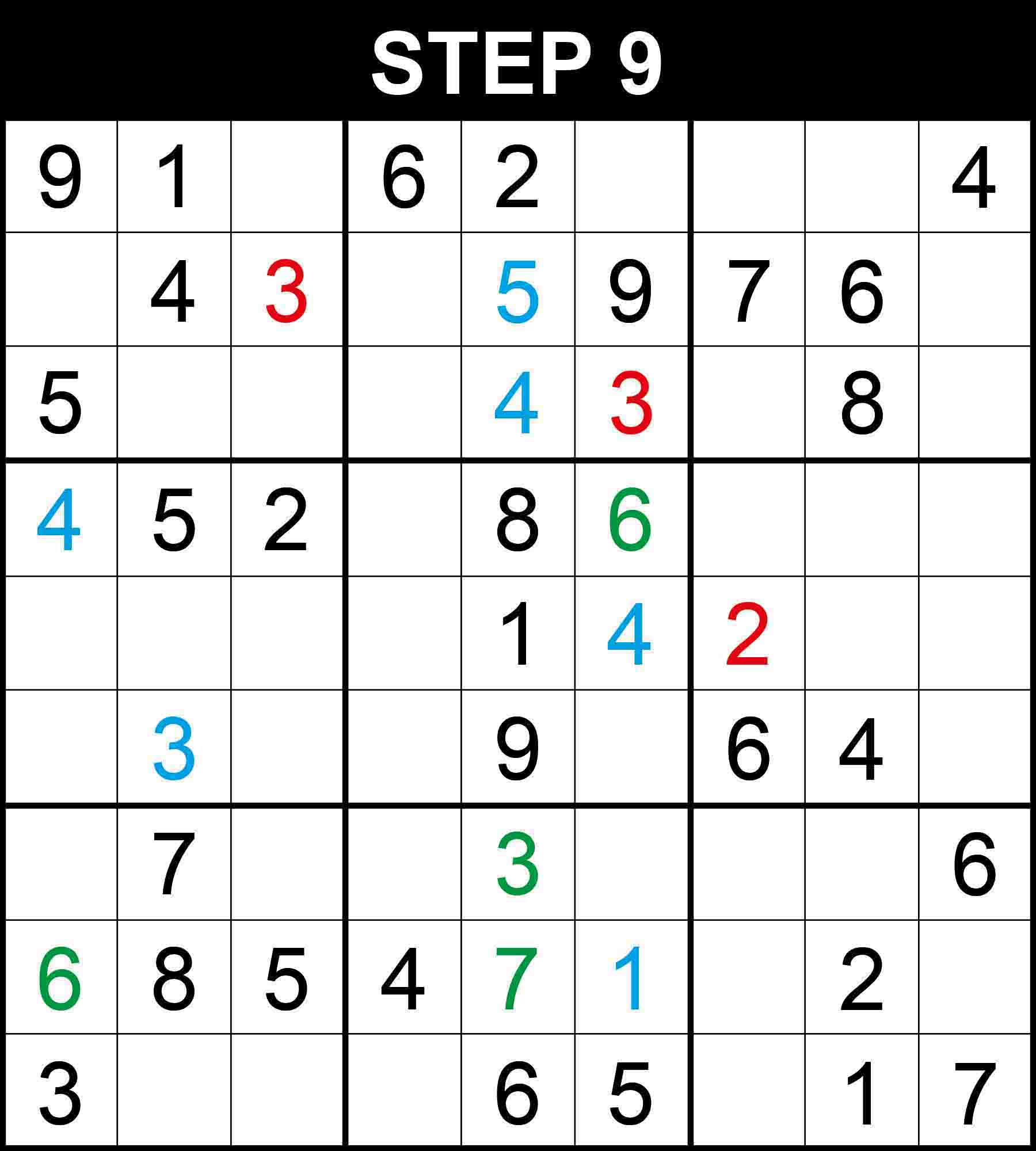
Cells (5,9) and (6,9) are the only positions for the candidates 5 and 8 in column 9 because the other cells in the column cannot contain 5 or 8. Therefore, There is a single position for 2 in box (2,3).
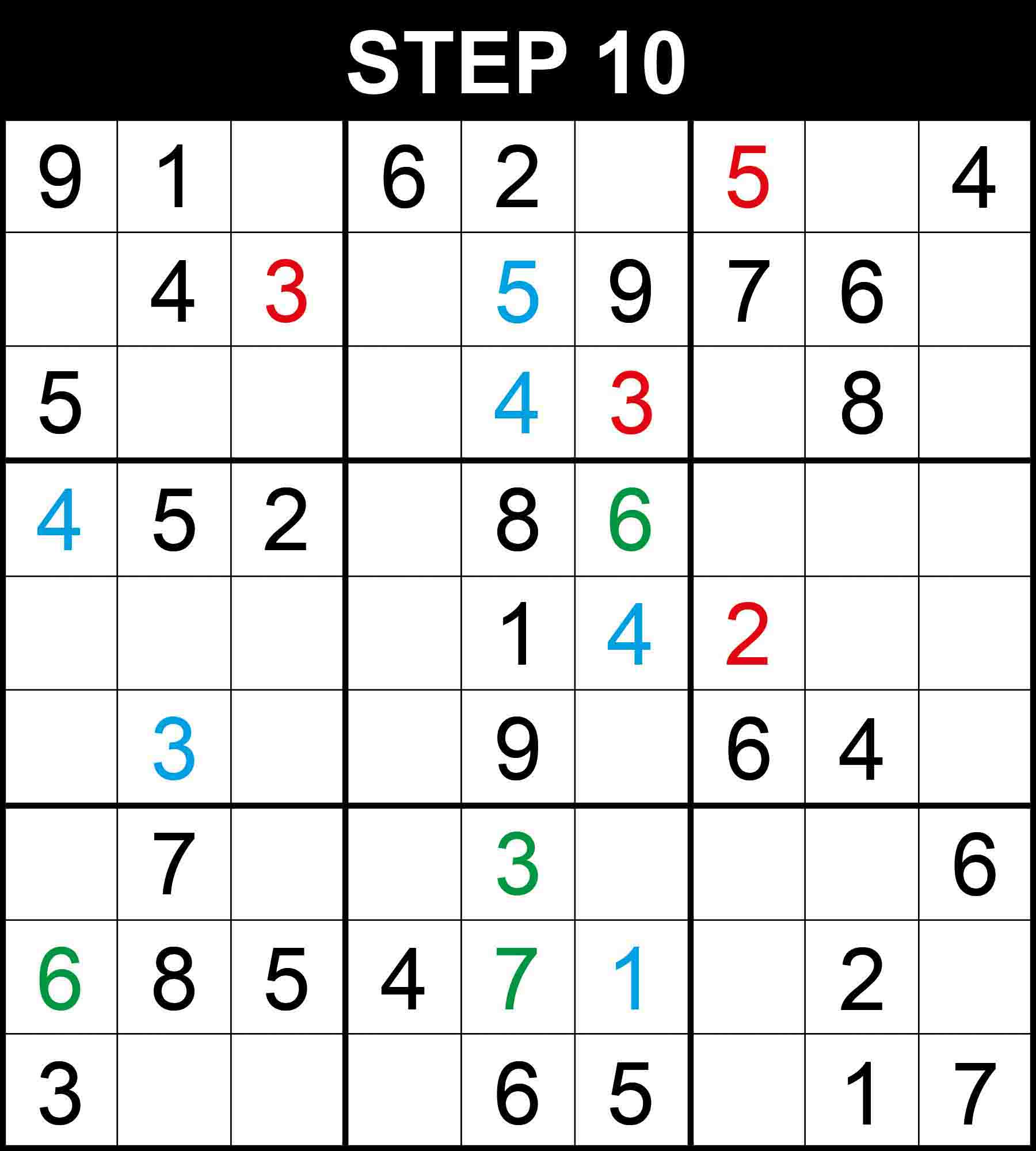
Cells (1,3) and (1,6) are the only positions for the candidates 7 and 8 in row 1. Cells (7,7) and (9,7) are the only positions for the candidates 4 and 8 in column 7. Because other cells in those dimensions cannot contain the pairs. Therefore, There is a single position for 5 in column 7.
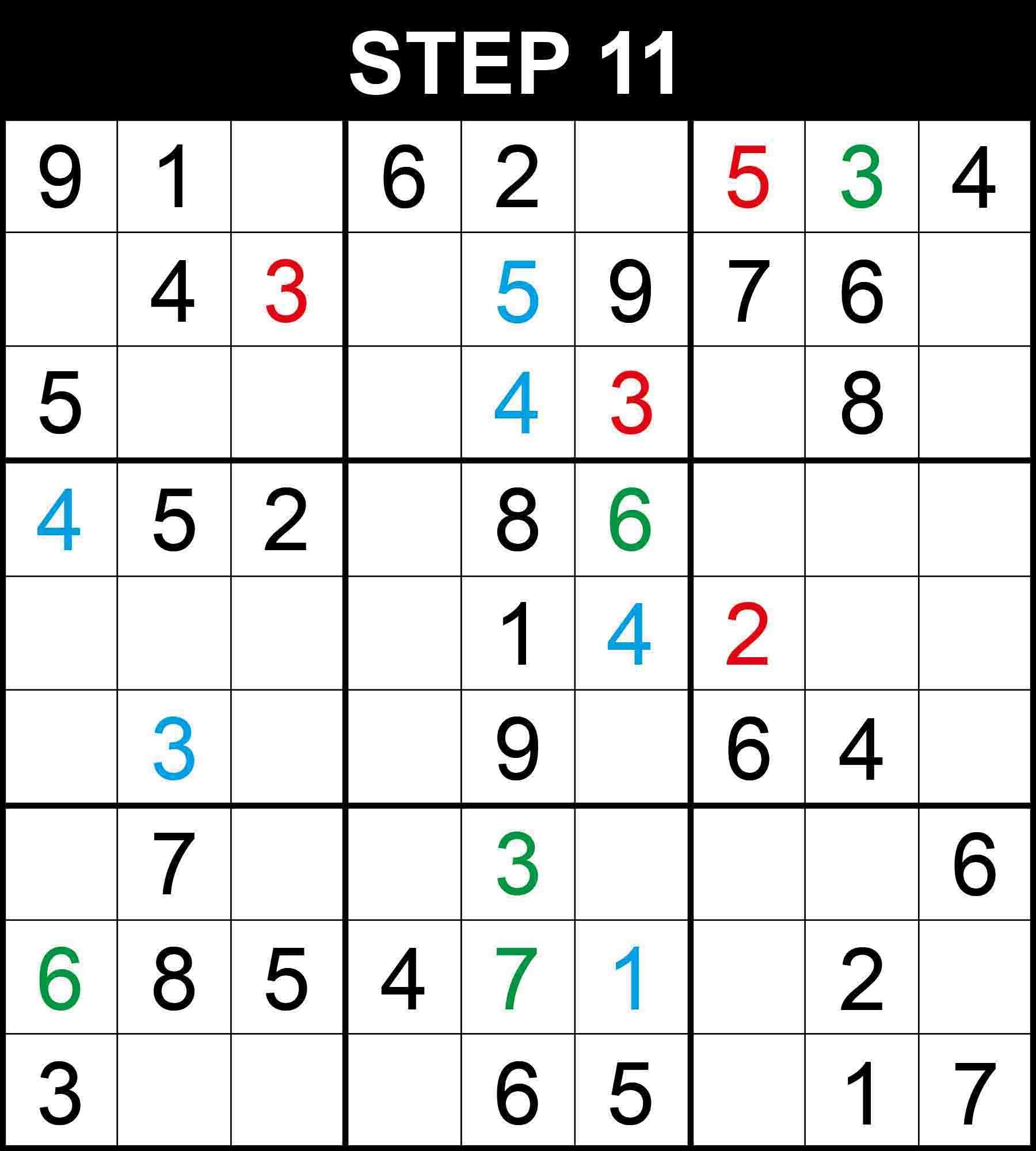
There is a single position for 3 in row 1. The other cells in the row cannot contain 3 because their columns already contain a 3.
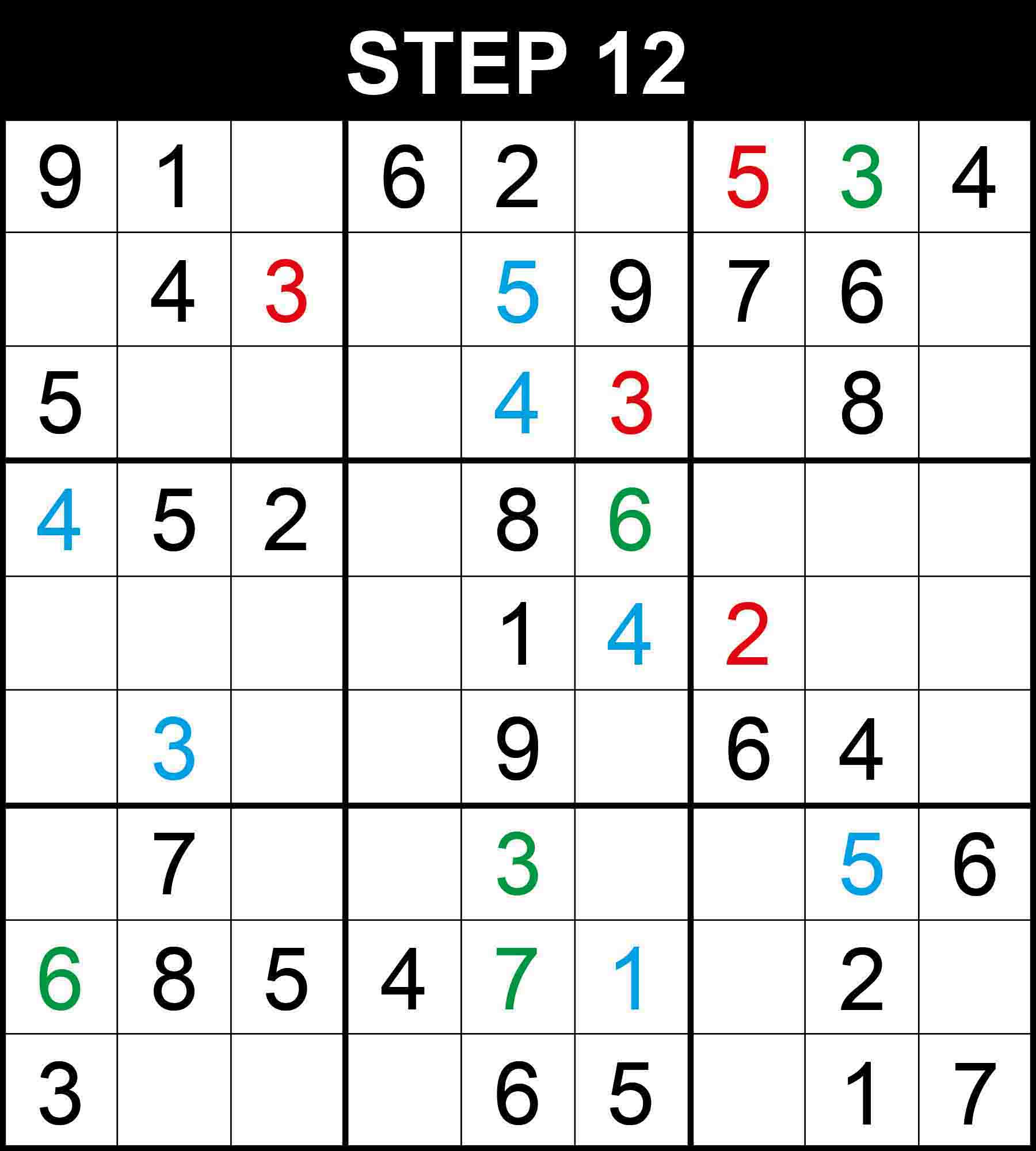
There is a single position for 5 in row 7. The other cells in the row cannot contain those numbers because their columns or boxes already contain a 5.
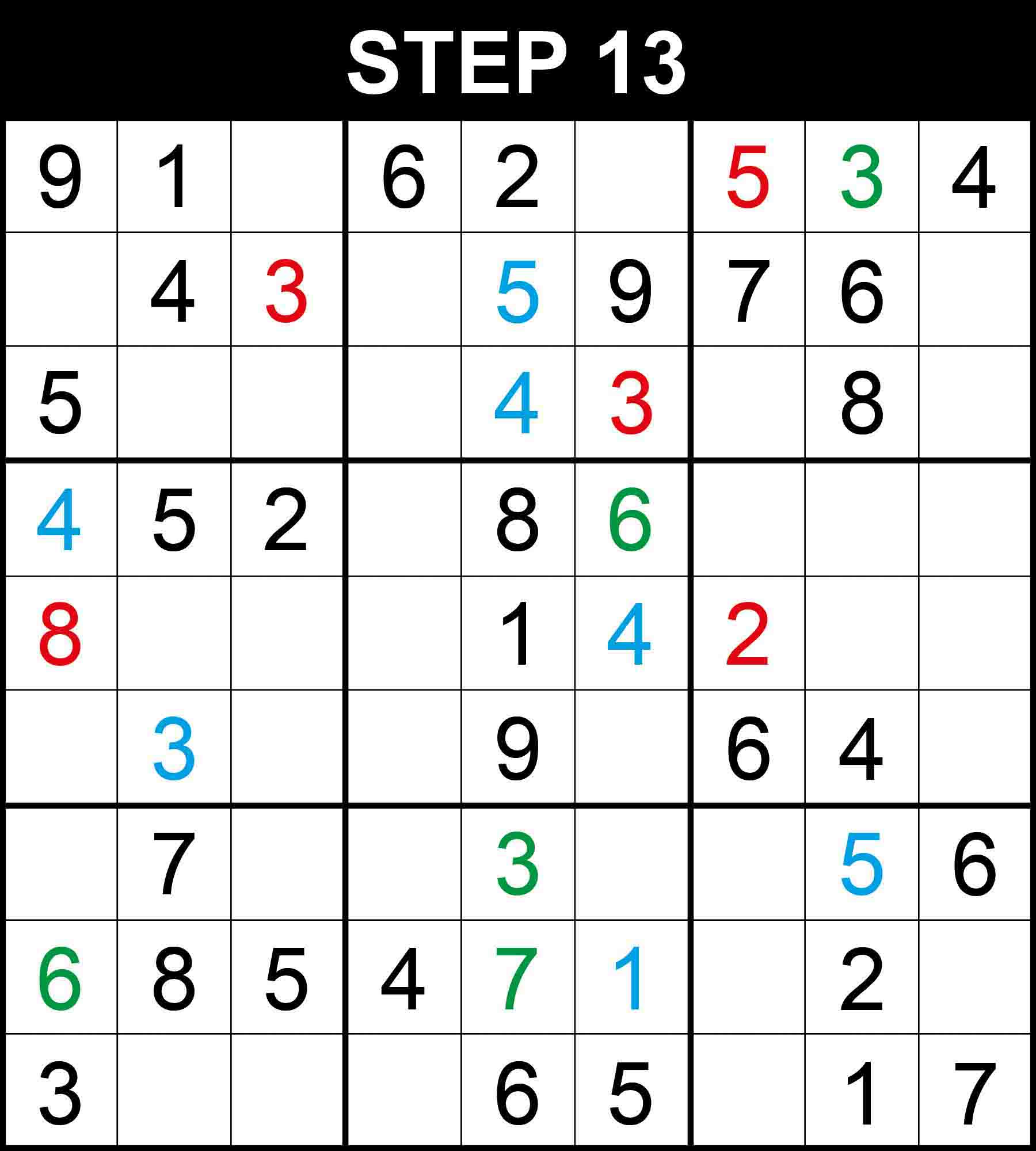
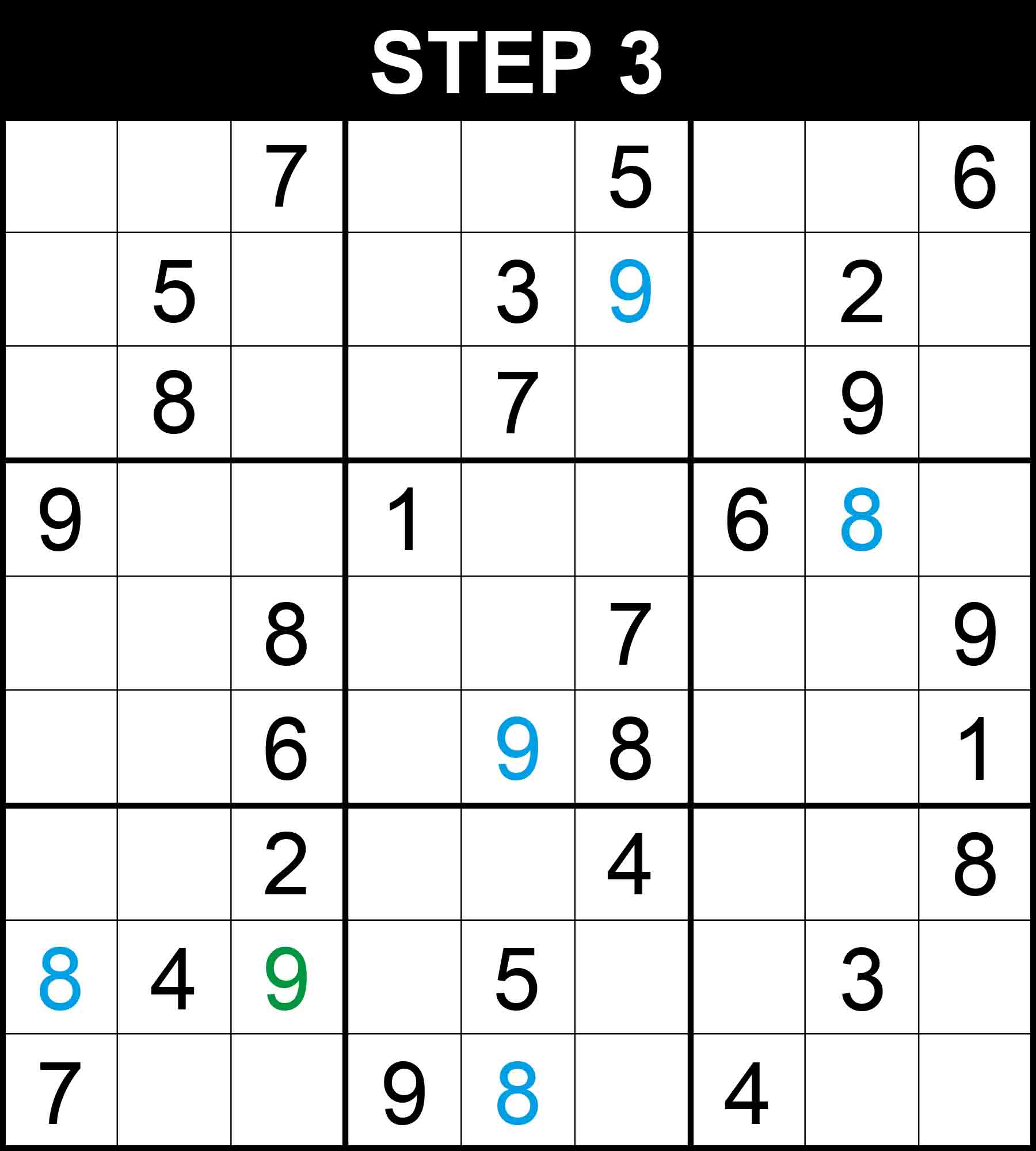
Cells (5,2) and (5,3) are the only positions for the candidates 6 and 9 in box (2,1). Cells (5,9) and (6,9) are the only positions for the candidates 5 and 8 in column 9. Because other cells in those dimensions cannot contain the pairs. Therefore, There is a single position for 8 in row 5.
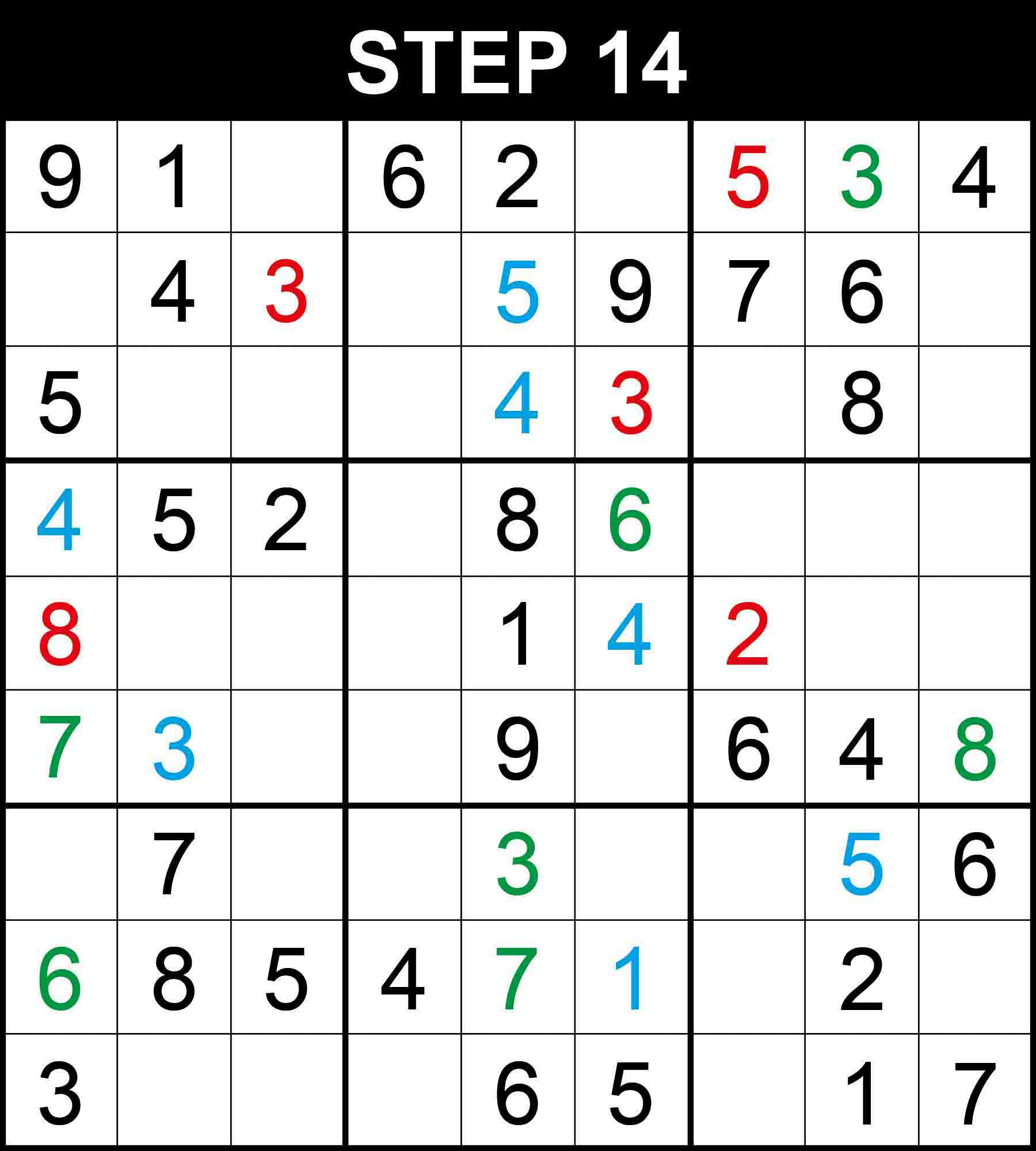
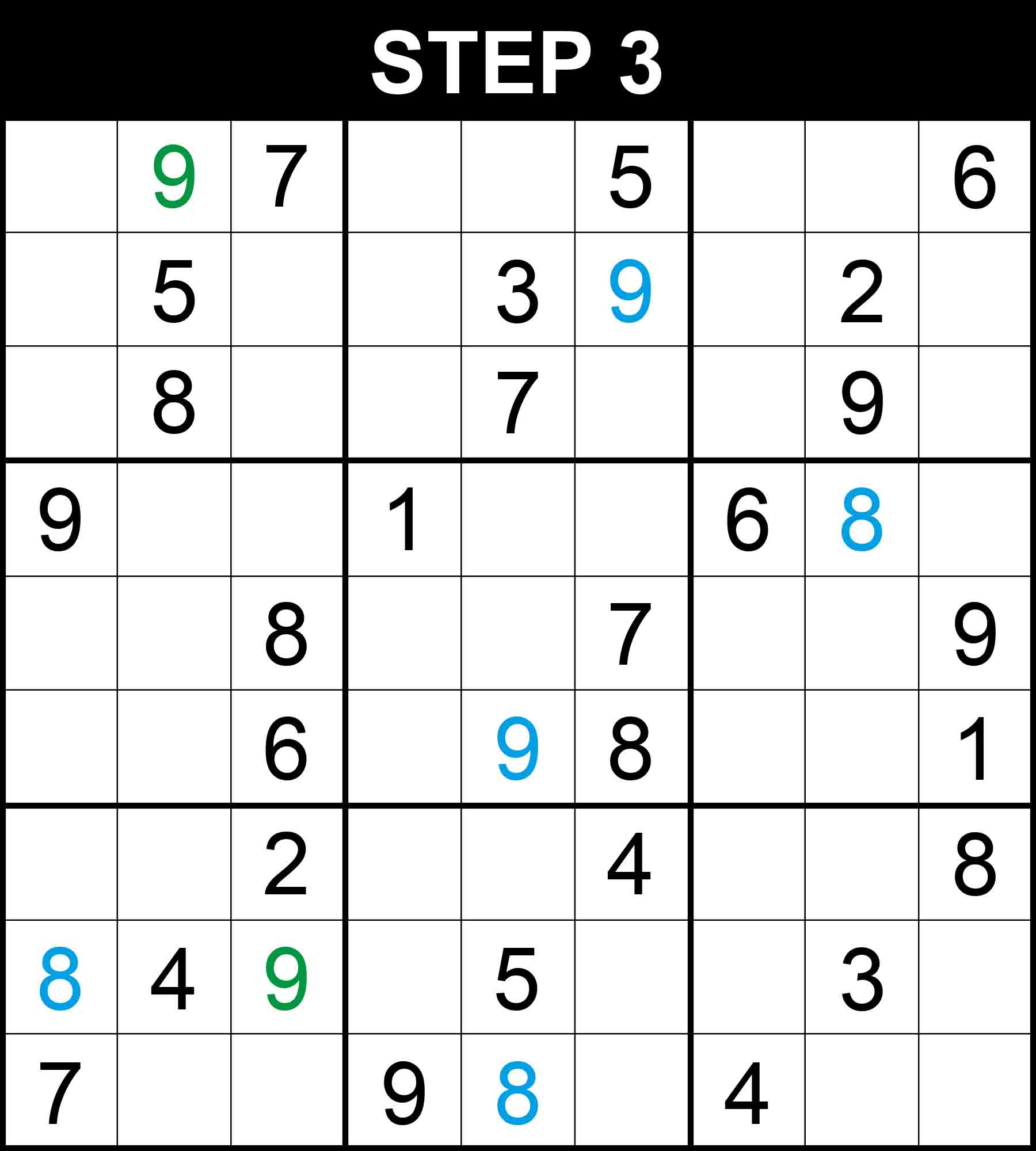
There is a single position for 8 in row 6, and 7 in column 1. The other cells in these dimensions cannot contain them because their rows, columns,, or boxes already contain them.
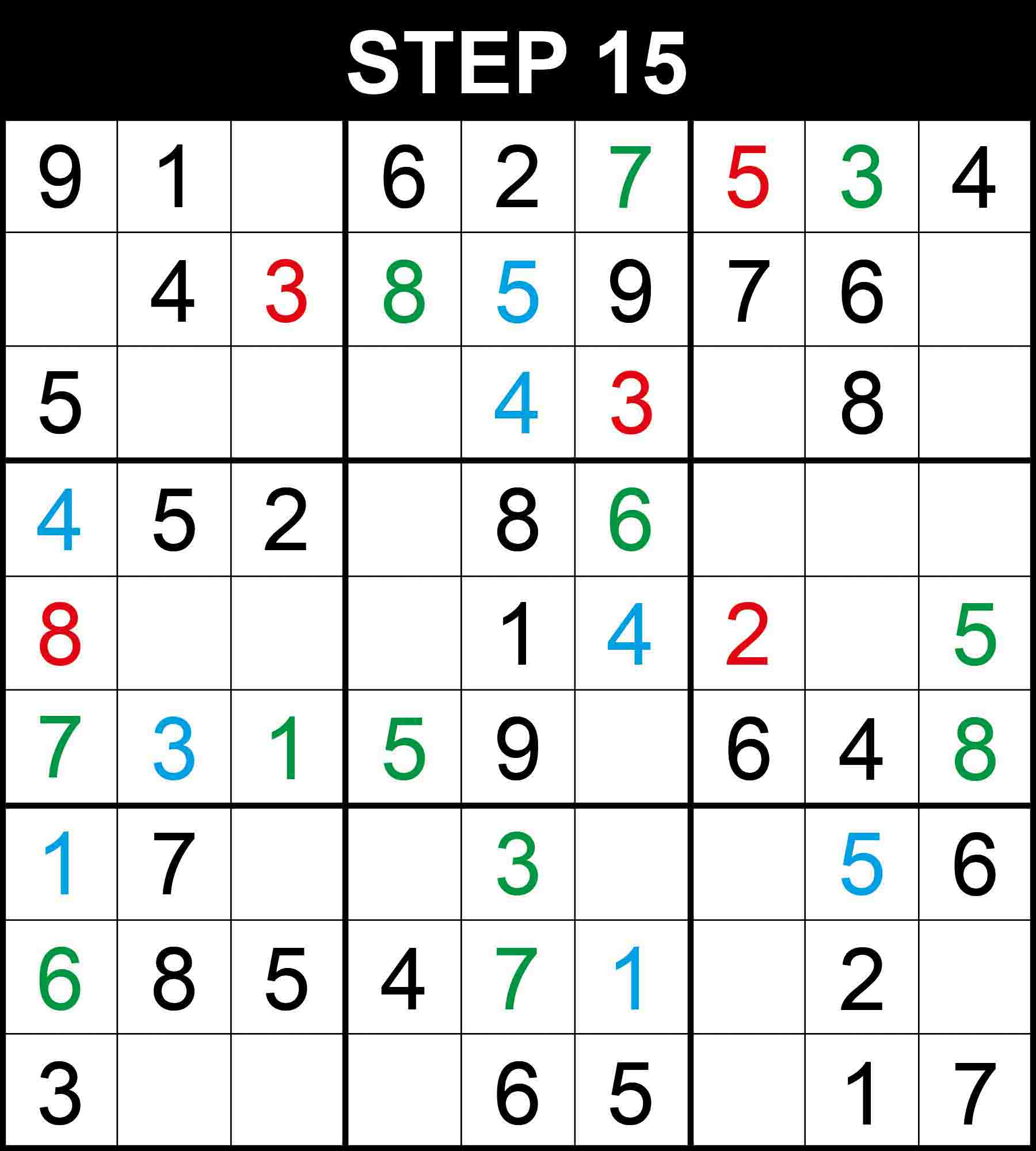
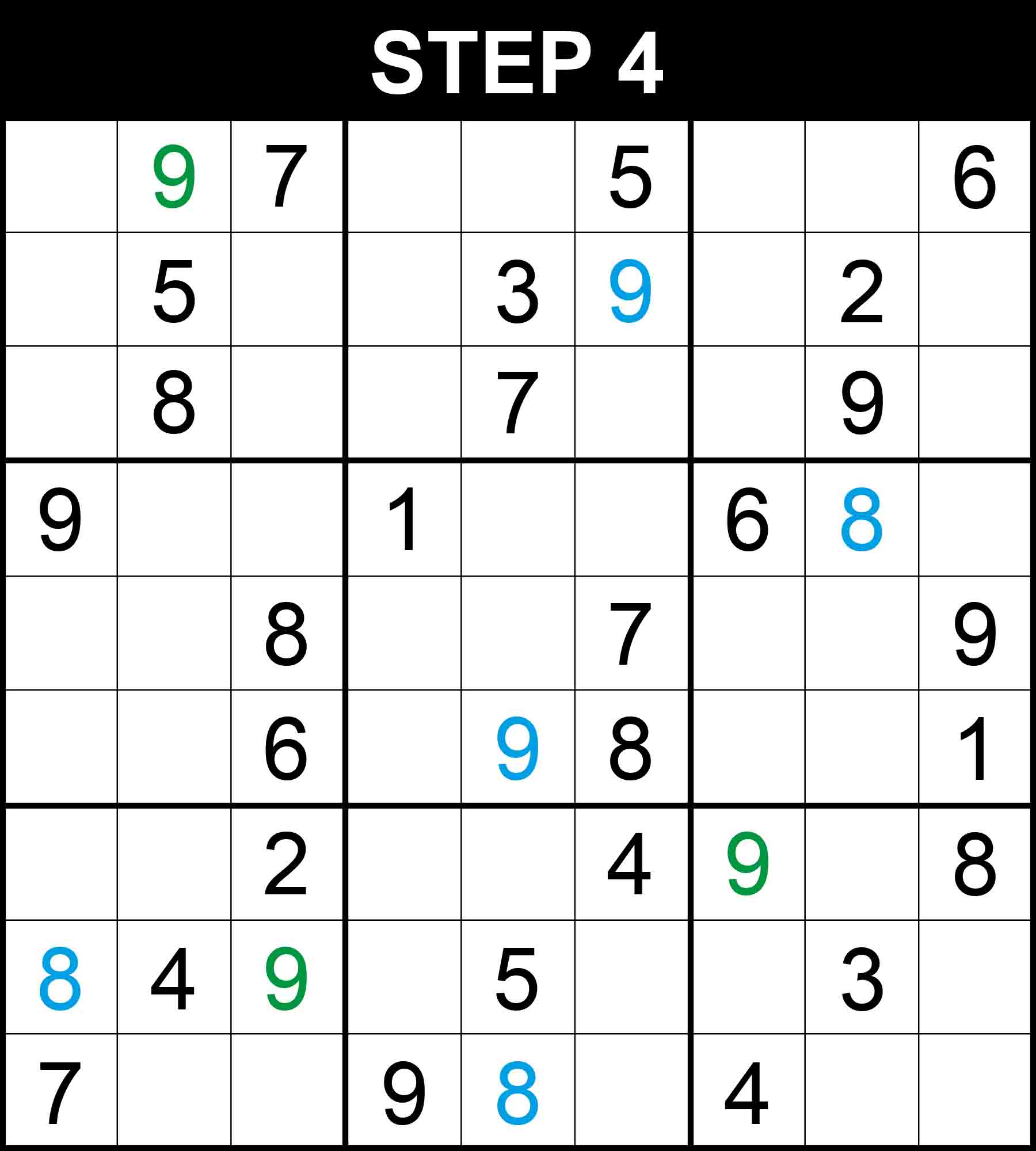
There is a single position for 8 in row 2, 1 in row 6, 5 in row 6, 1 in column 1, 7 in column 6, 5 in column 9. The other cells in these dimensions cannot contain them because their rows, columns, or boxes already contain them.
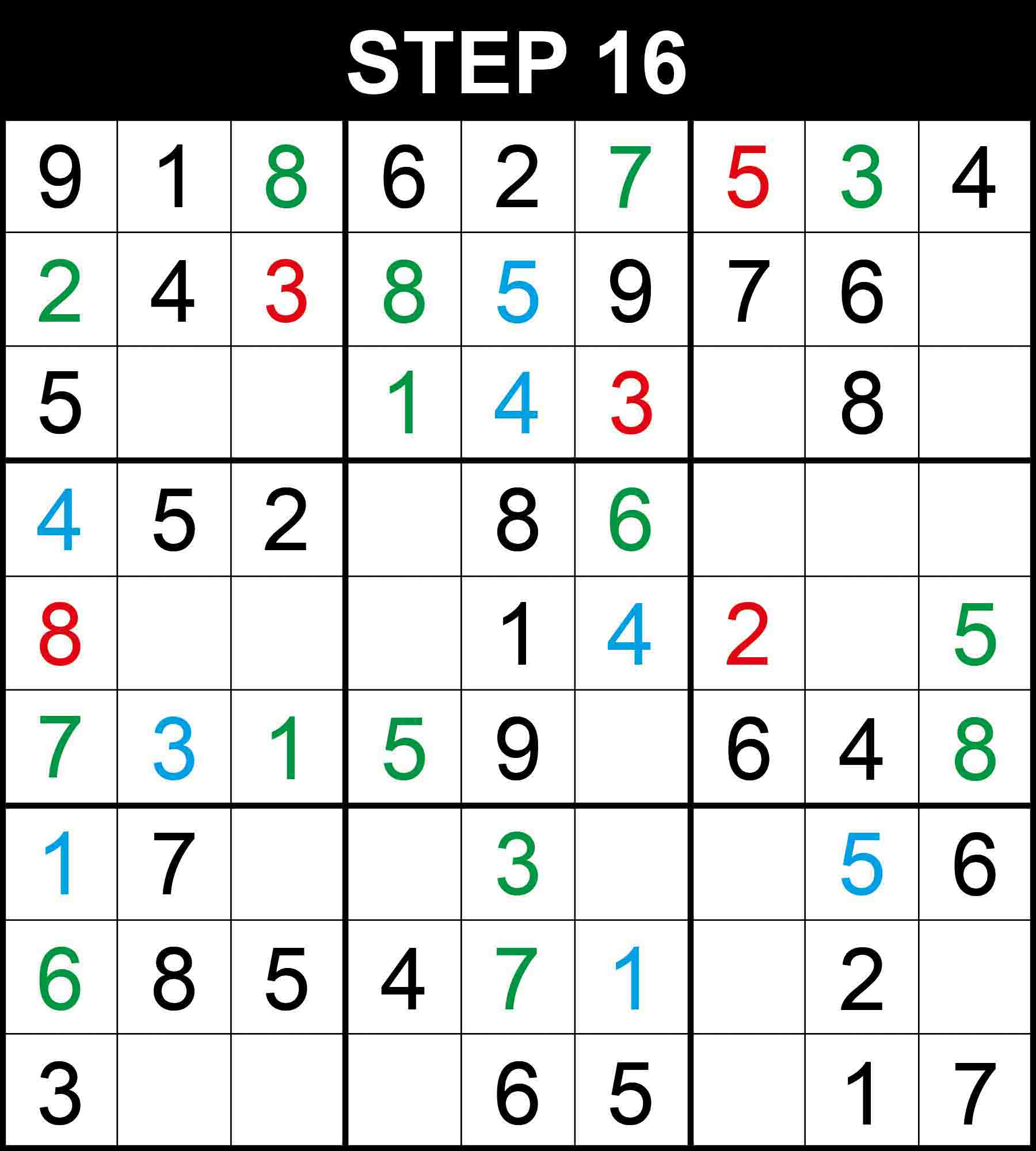
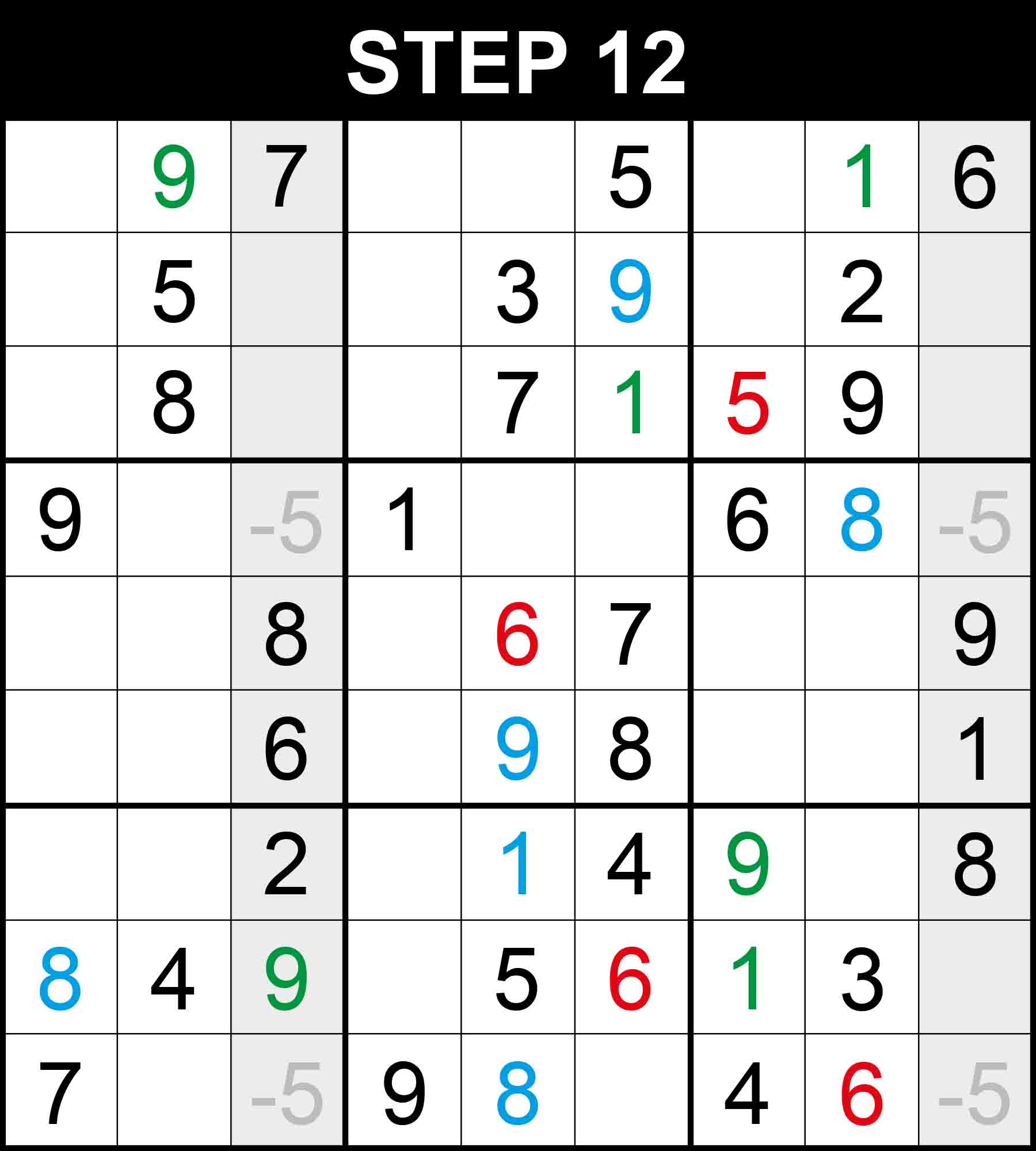
Looking at row 1, 8 is the only missing value at (1,3). Looking at row 6, 2 is the only missing value at (6,6). Looking at column 1, 2 is the only missing value at (2,1). Looking at box (1,2), 1 is the only missing value at (3,4).
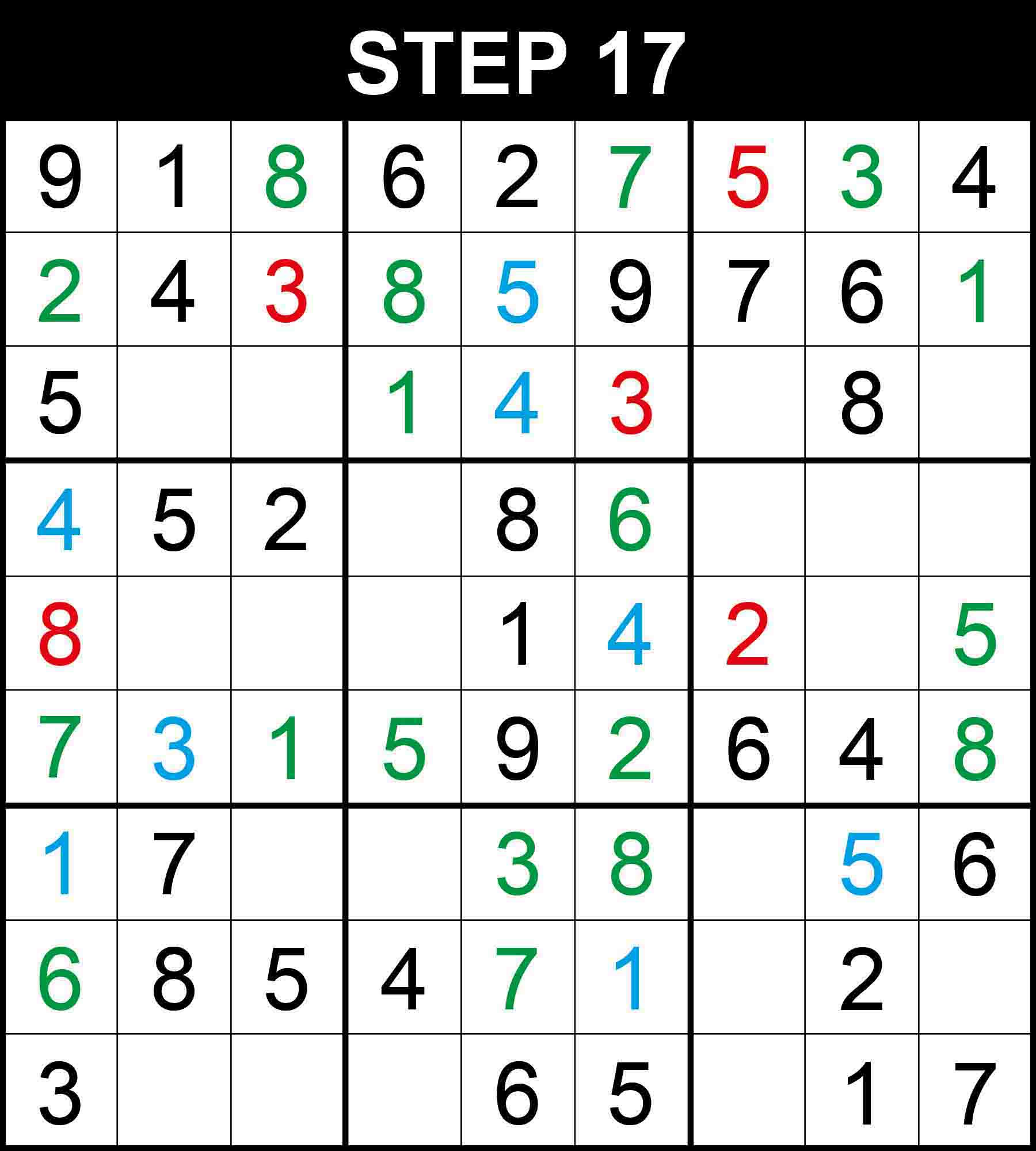
Looking at row 2, 1 is the only missing value at (2,9). Looking at column 6, 8 is the only missing value at (7,6).
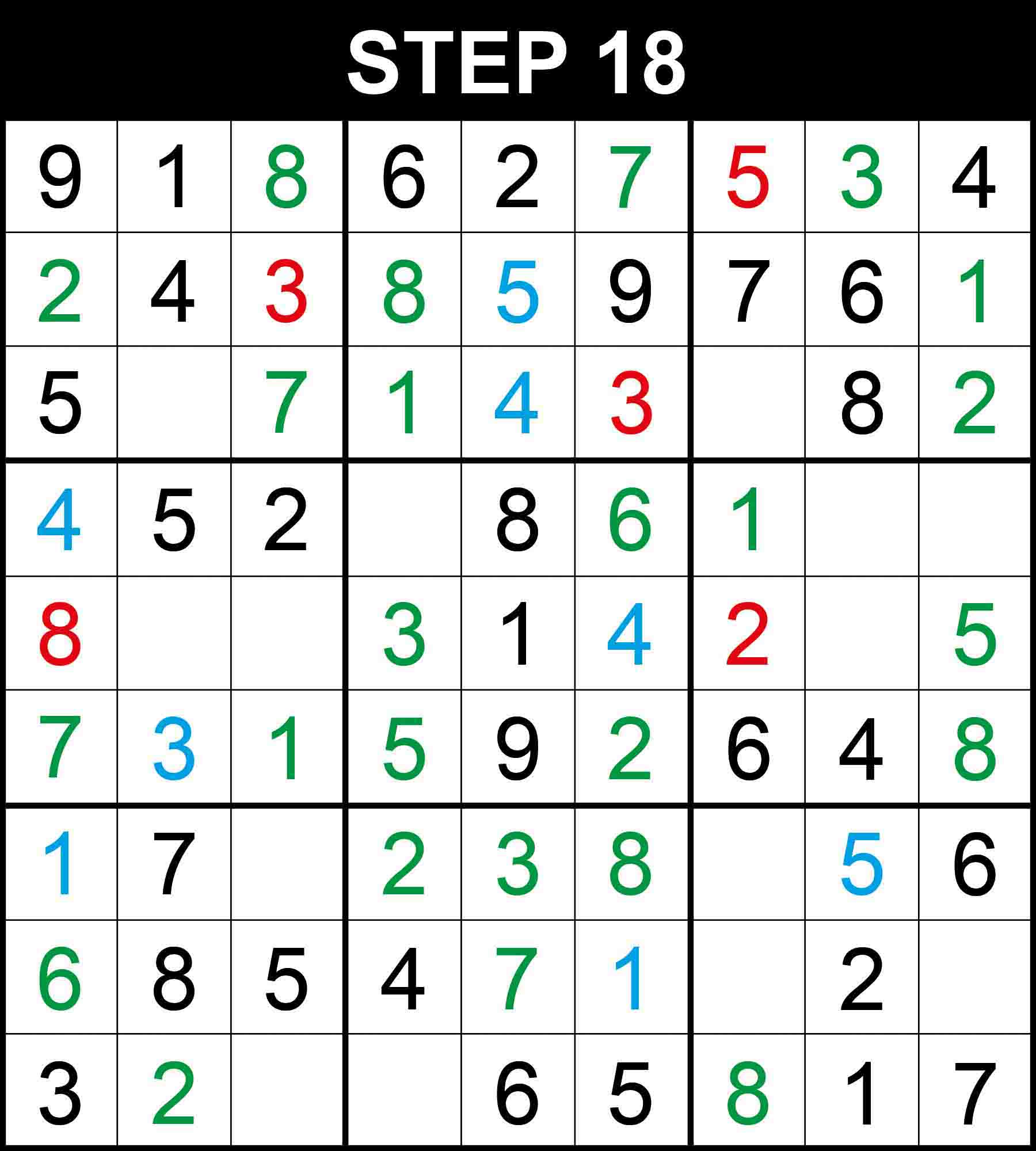
There is a single position for 7 in row 3, 1 in row 4, 3 in row 5, 2 in row 7, 8 in row 9, 2 in column 2, 2 in column 9. The other cells in these dimensions cannot contain them because their rows, columns, or boxes already contain them.
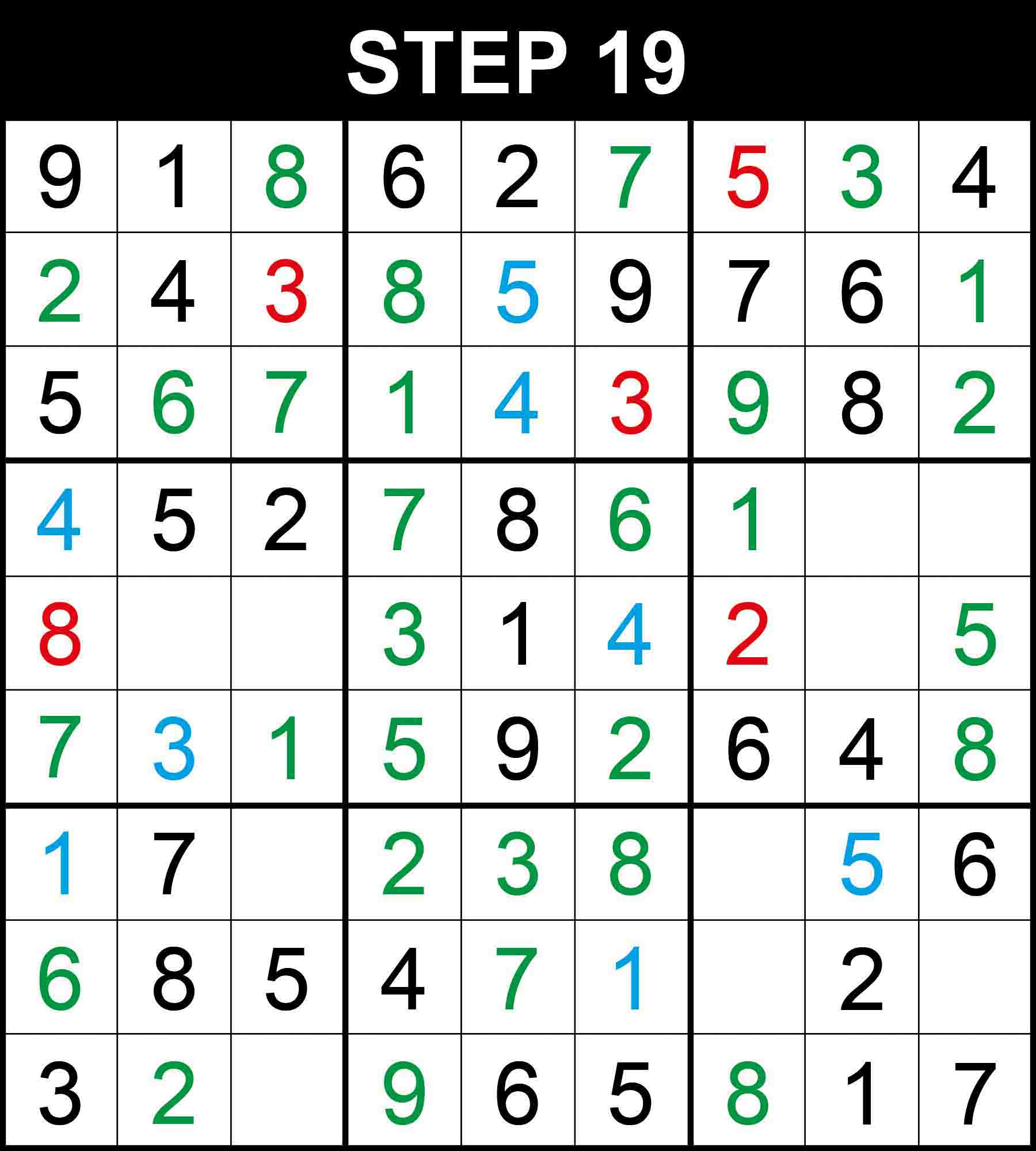
Looking at box (1,1), 6 is the only missing value at (3,2). Looking at box (1,3), 9 is the only missing value at (3,7). Looking at box (2,2), 7 is the only missing value at (4,4). Looking at box (3,2), 9 is the only missing value at (9,4).
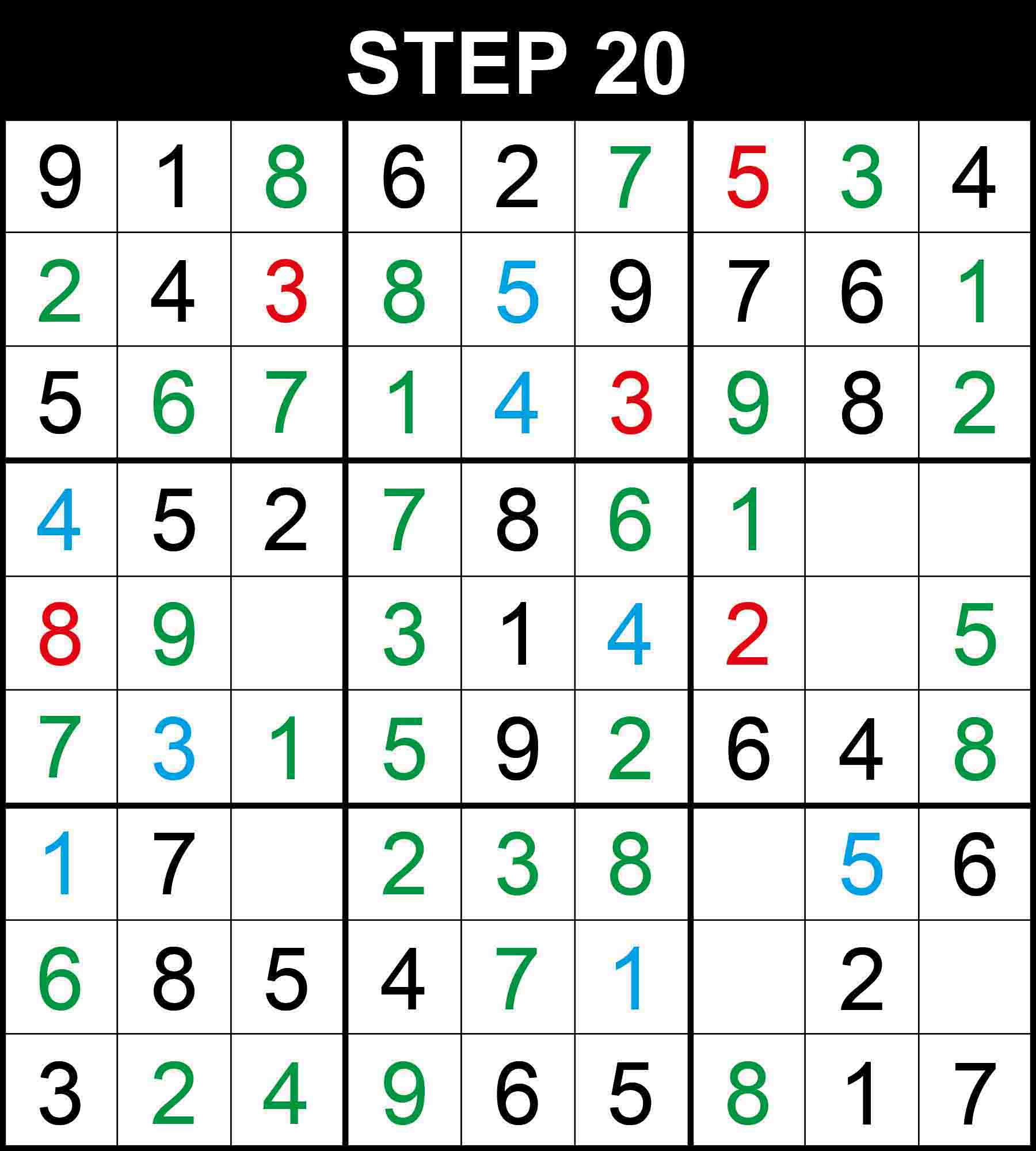
Looking at row 9, 4 is the only missing value at (9,3). Looking at column 2, 9 is the only missing value at (5,2).
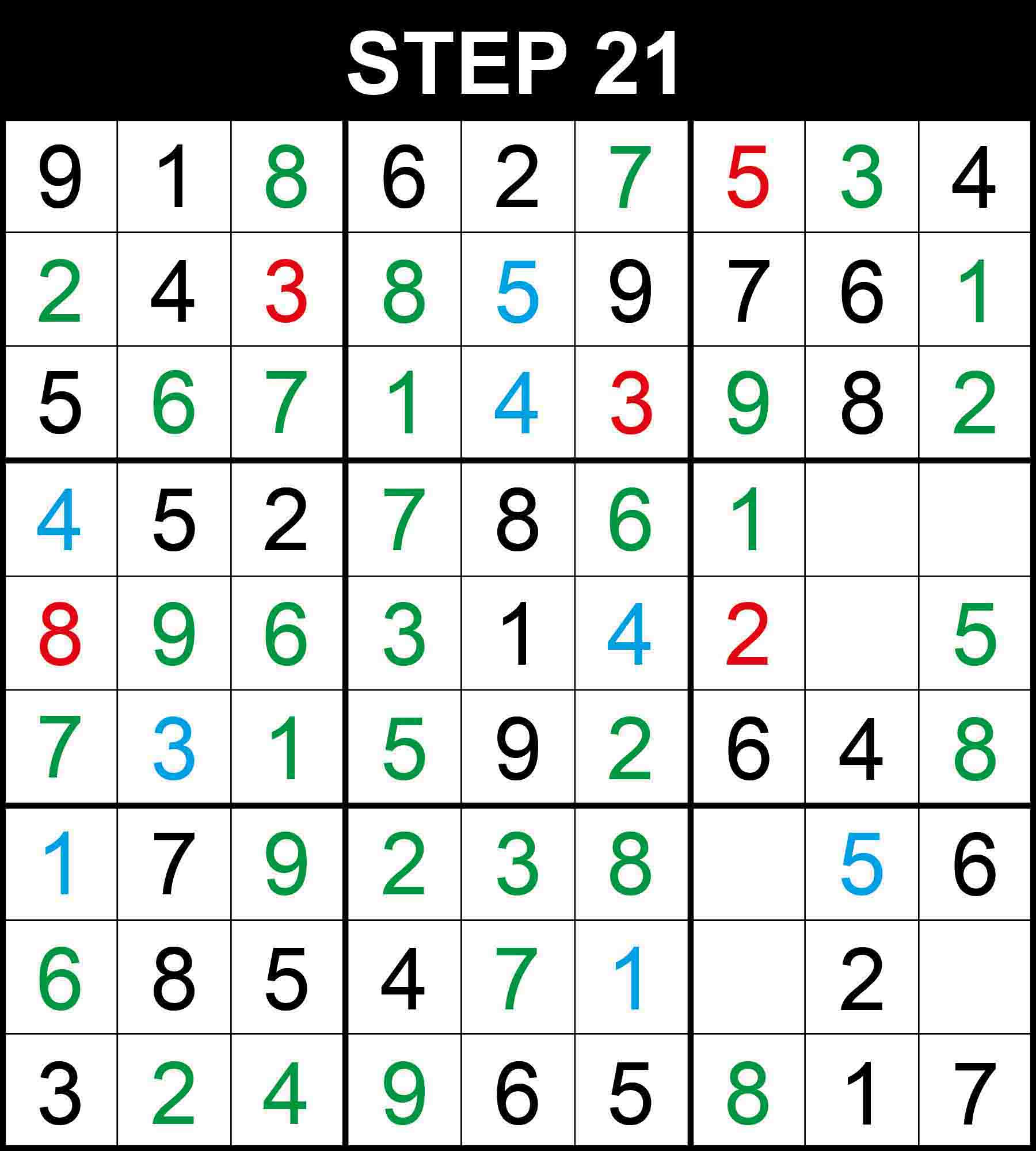
Looking at box (2,1), 6 is the only missing value at (5,3). Looking at box (3,1), 9 is the only missing value at (7,3).
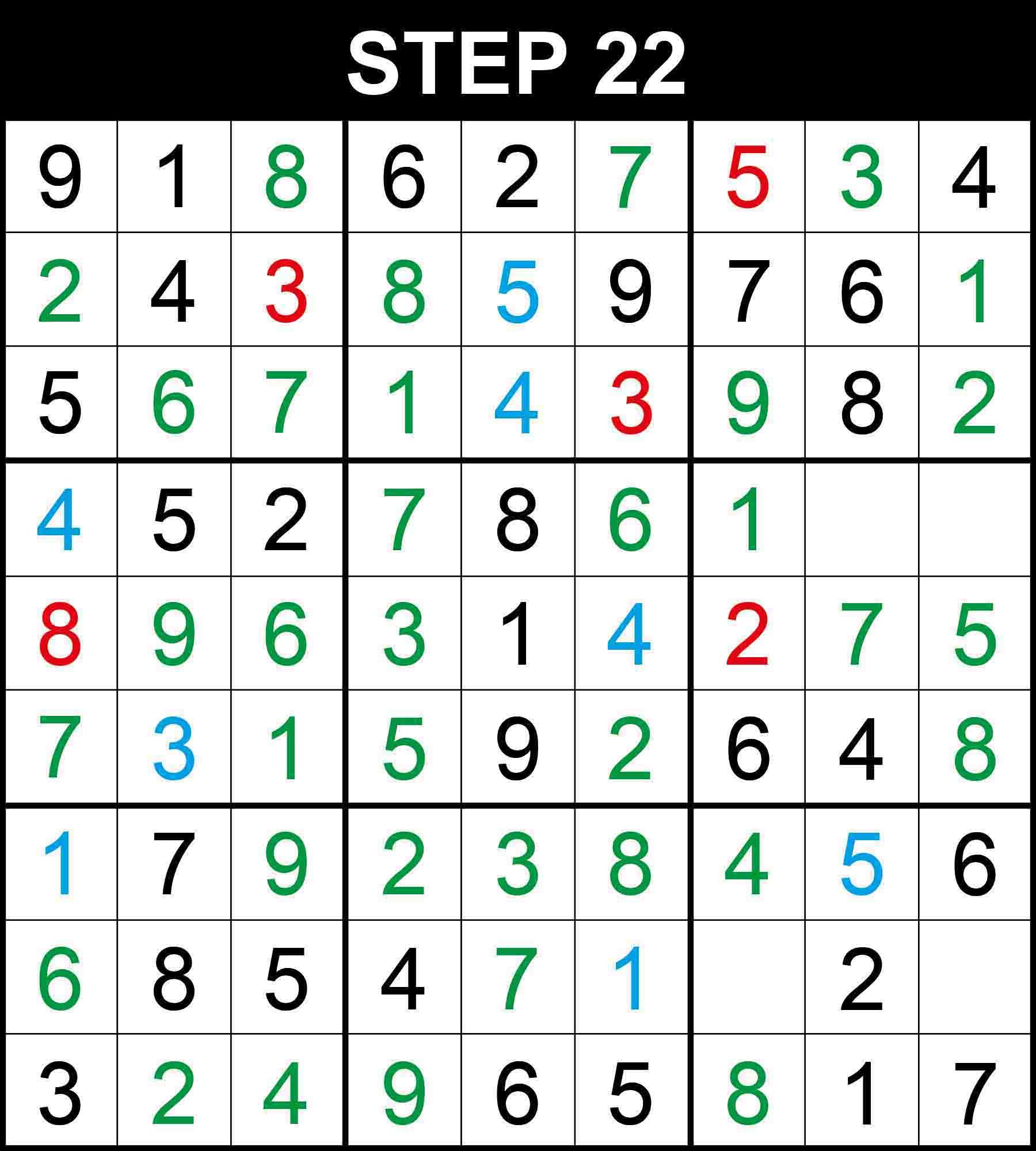
Looking at row 5, 7 is the only missing value at (5,8). Looking at row 7, 4 is the only missing value at (7,7).
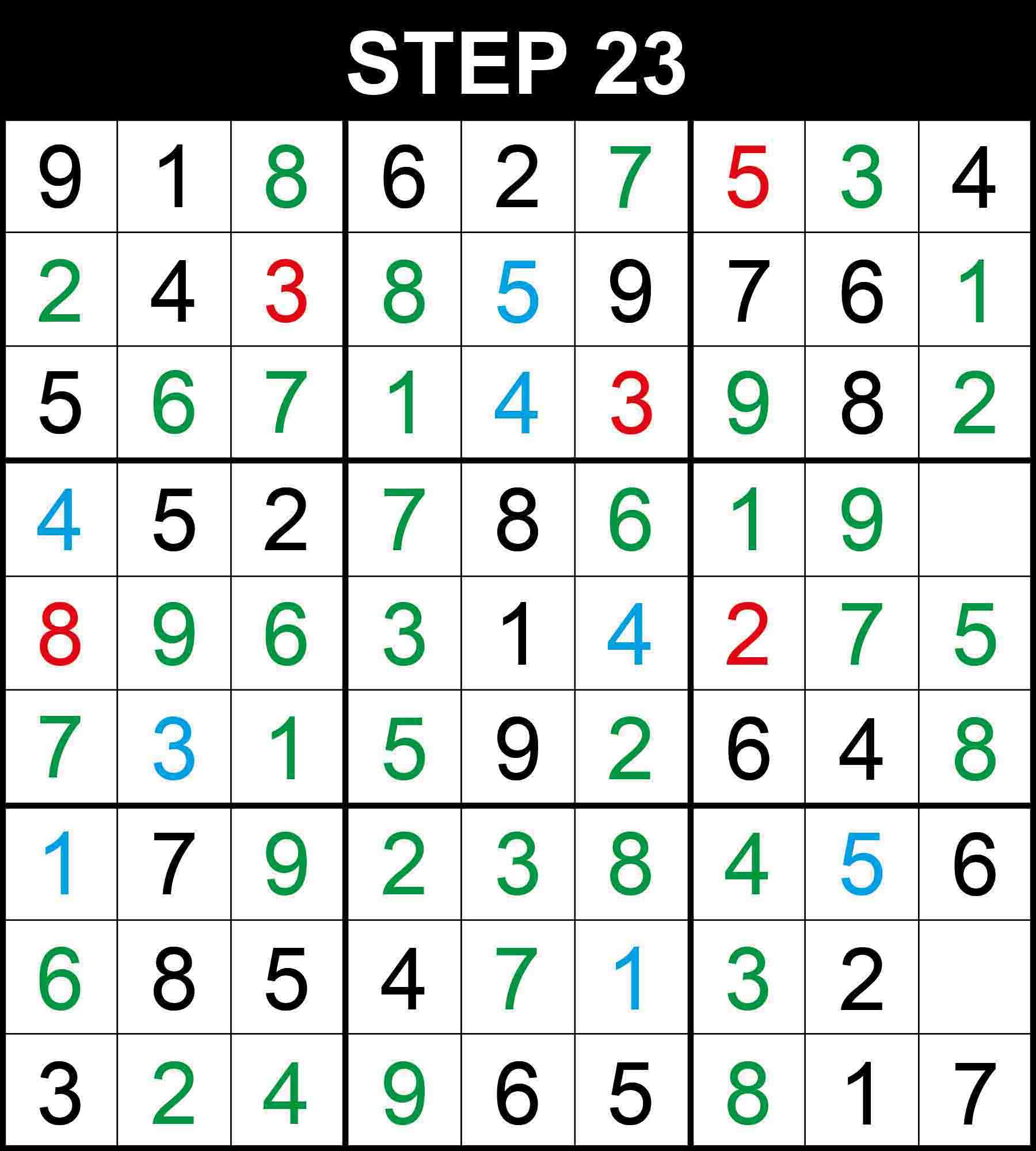
Looking at column 7, 3 is the only missing value at (8,7). Looking at column 8, 9 is the only missing value at (4,8).
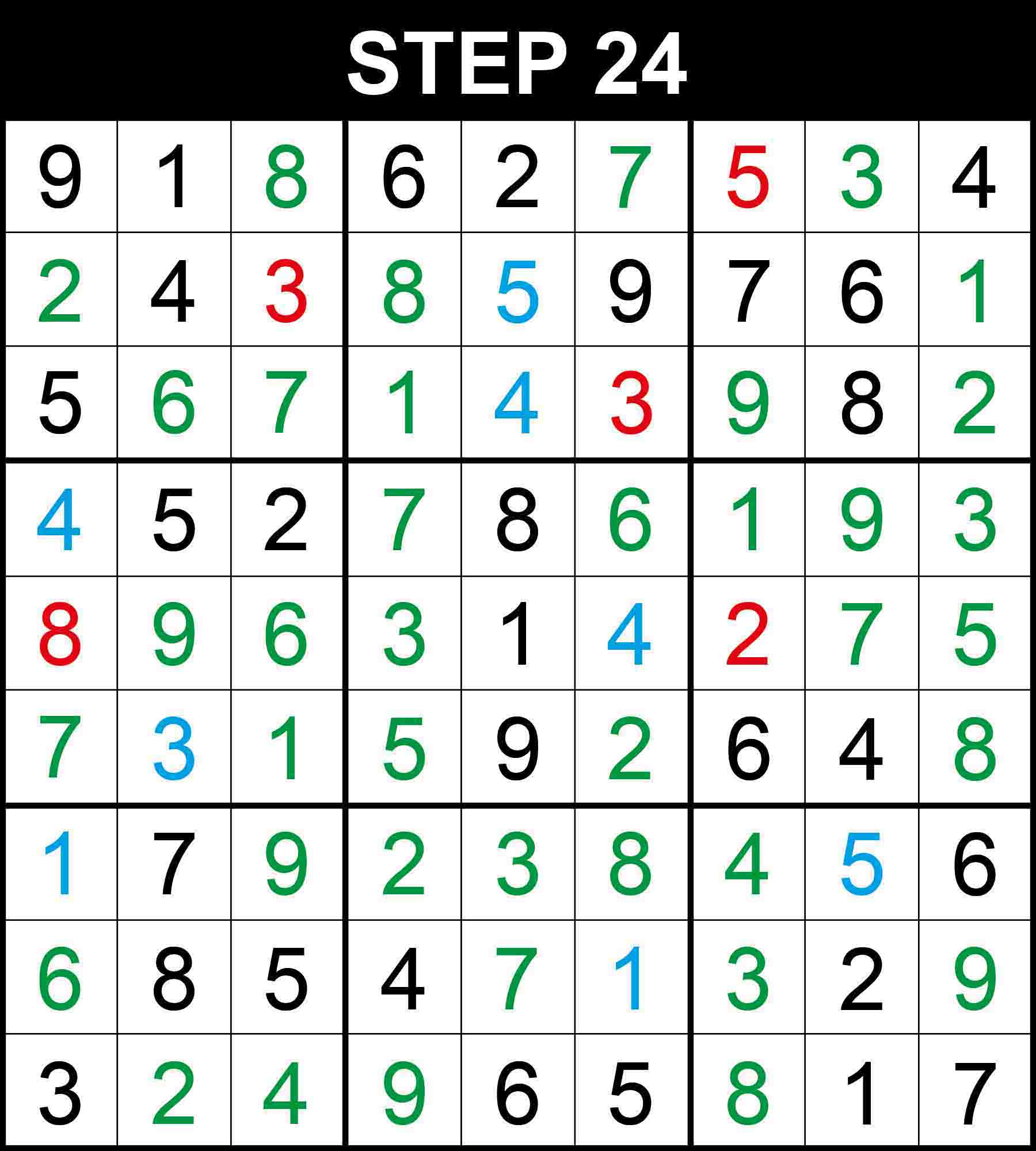
Looking at row 4, 3 is the only missing value at (4,9). Looking at row 8, 9 is the only missing value at (8,9). The puzzle is now complete!
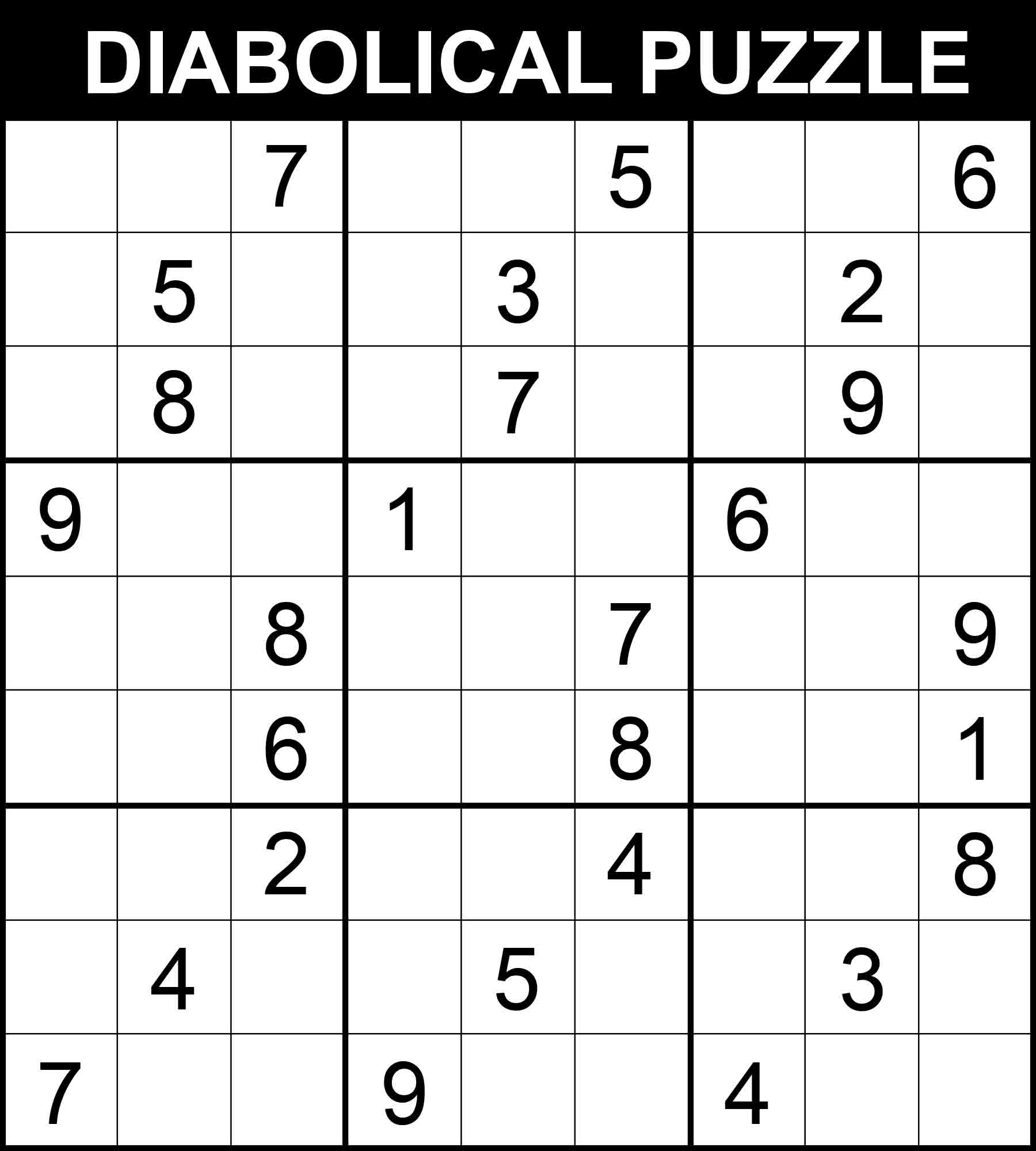
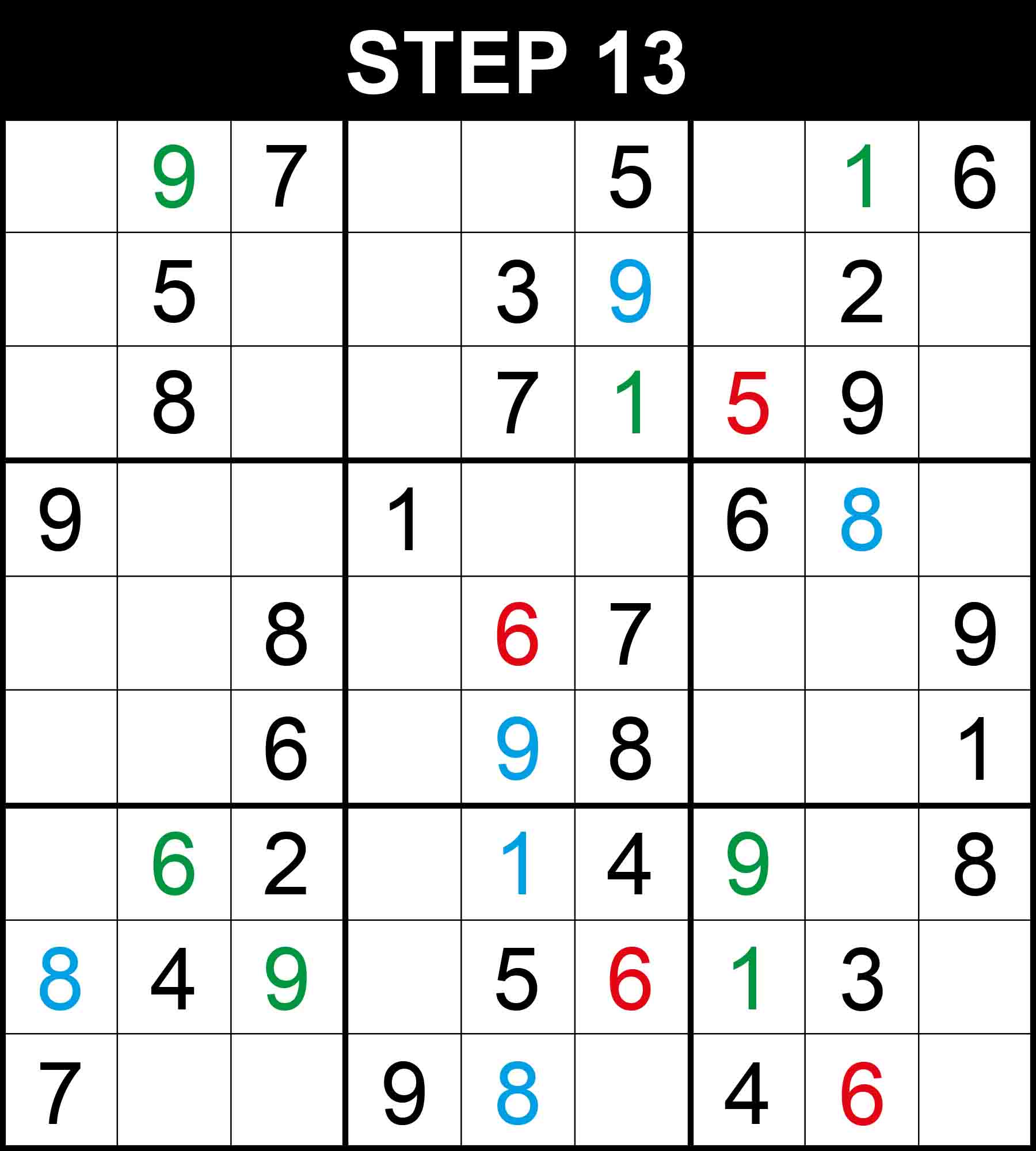
With 27 hints only and 7 hard steps where you may potentially get stuck at, this puzzle can be considered a very challenging puzzle. It is in the category of what is sometimes referred to as diabolical Sudoku puzzles. Let’s follow its step-by-step solution in 30 steps. New values found through an easy step are highlighted in green, those found through a medium step are written in blue, and those found through a hard step are presented in red.
Note: This puzzle comes from one of our challenging Sudoku books. It is the last and most challenging Sudoku puzzle in the book Very Hard Sudoku. All 340 puzzles in the book have an easily accessible step-by-step solution. You can get a copy on Amazon and solve 340 challenging puzzles by following this link.
There is a single position for 8 in row 4, 9 in row 6, 8 in row 9, 8 in column 1, and 9 in column 6. The other cells in these dimensions cannot contain those numbers because their rows, columns, or boxes already contain them.
There is a single position for 9 in column 3. The other cells in this dimension cannot contain 9 because their rows, columns, or boxes already contain 9.
There is a single position for 9 in column 2. The other cells in this dimension cannot contain 9 because their rows, columns, or boxes already contain 9.
There is a single position for 9 in row 7. The other cells in this dimension cannot contain 9 because their rows, columns, or boxes already contain 9.
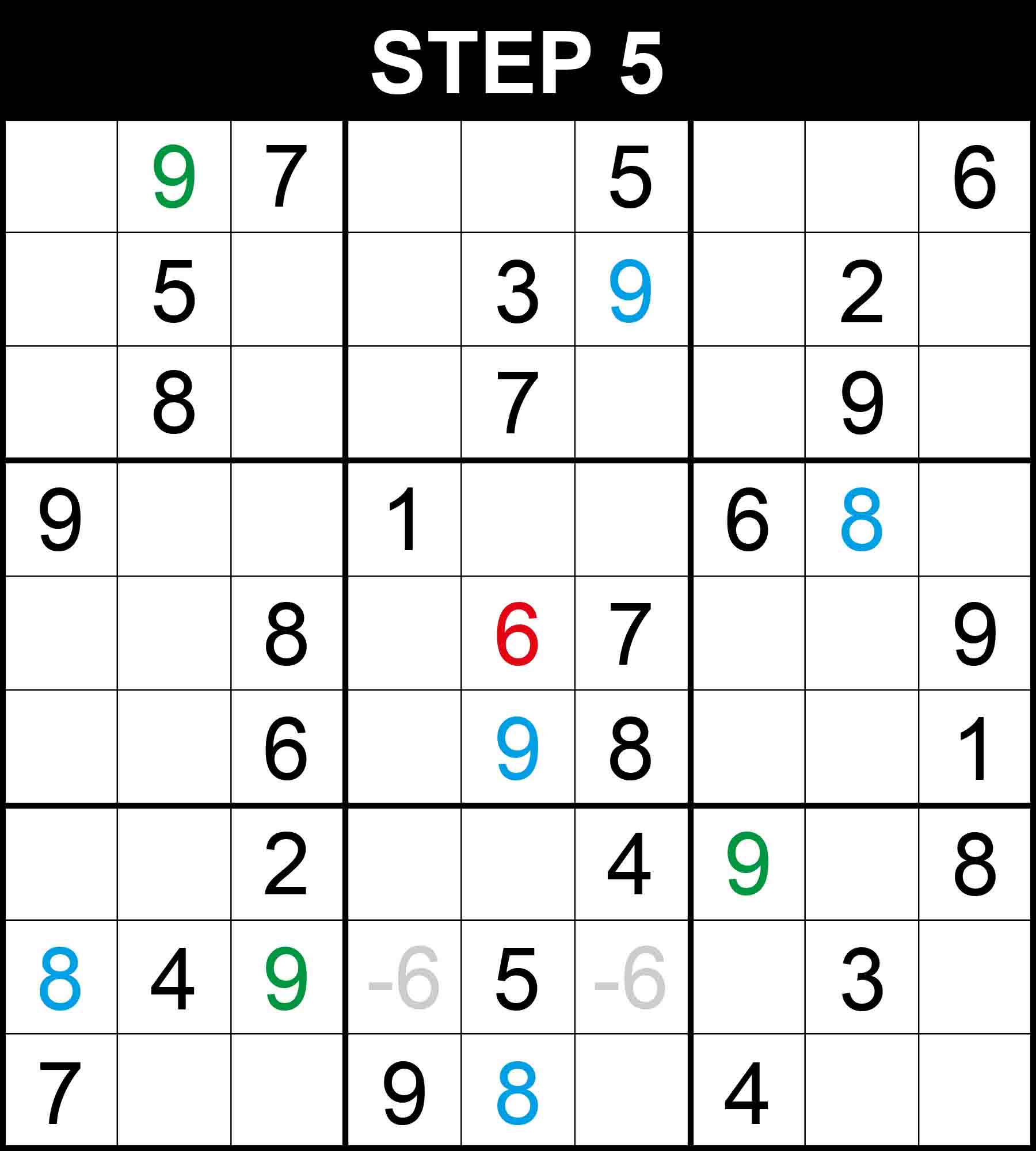
There is a single position for 9 in column 2. The other cells in this dimension cannot contain 9 because their rows, columns, or boxes already contain 9.
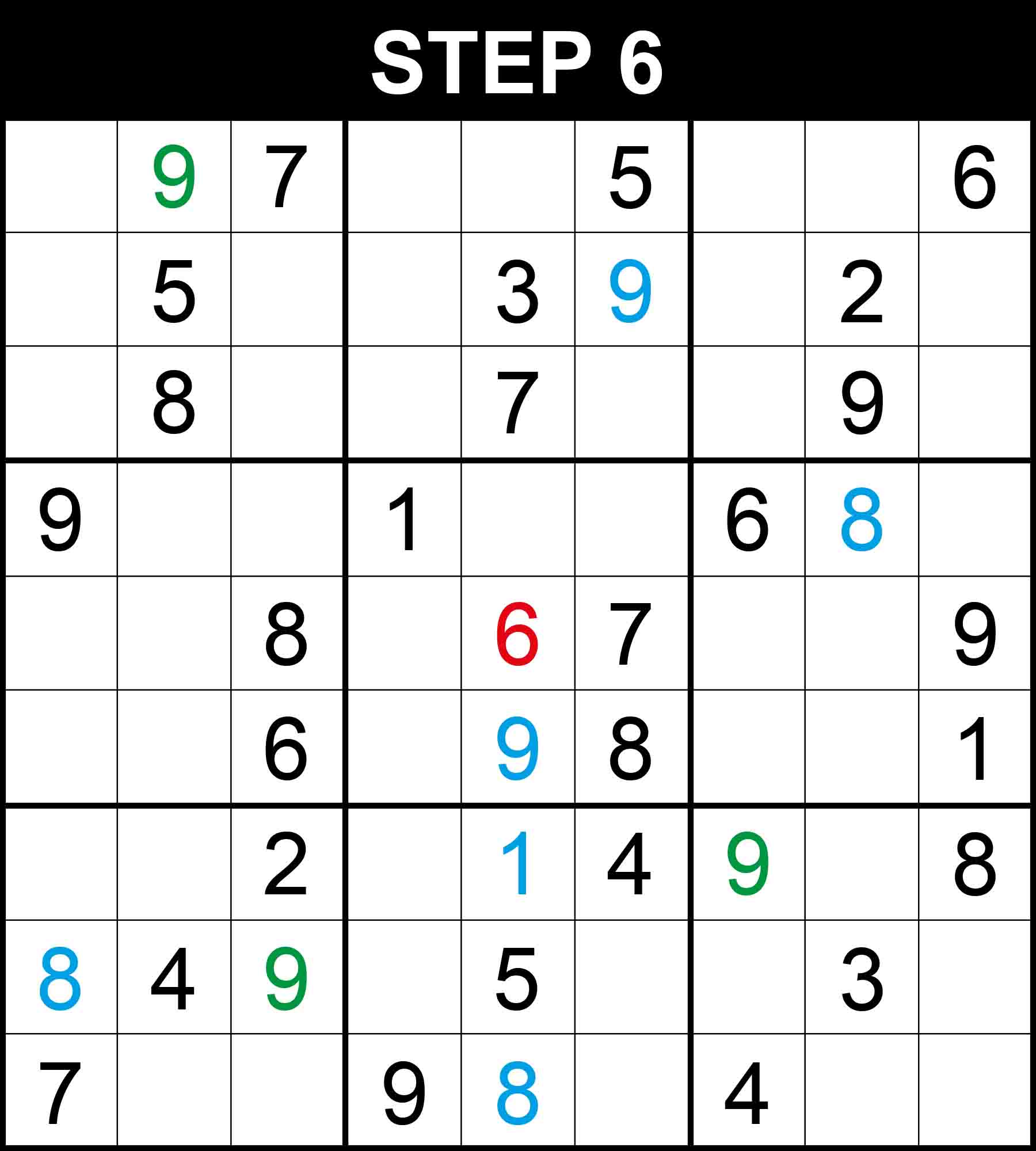
There is a single position for 9 in row 7. The other cells in this dimension cannot contain 9 because their rows, columns, or boxes already contain 9.
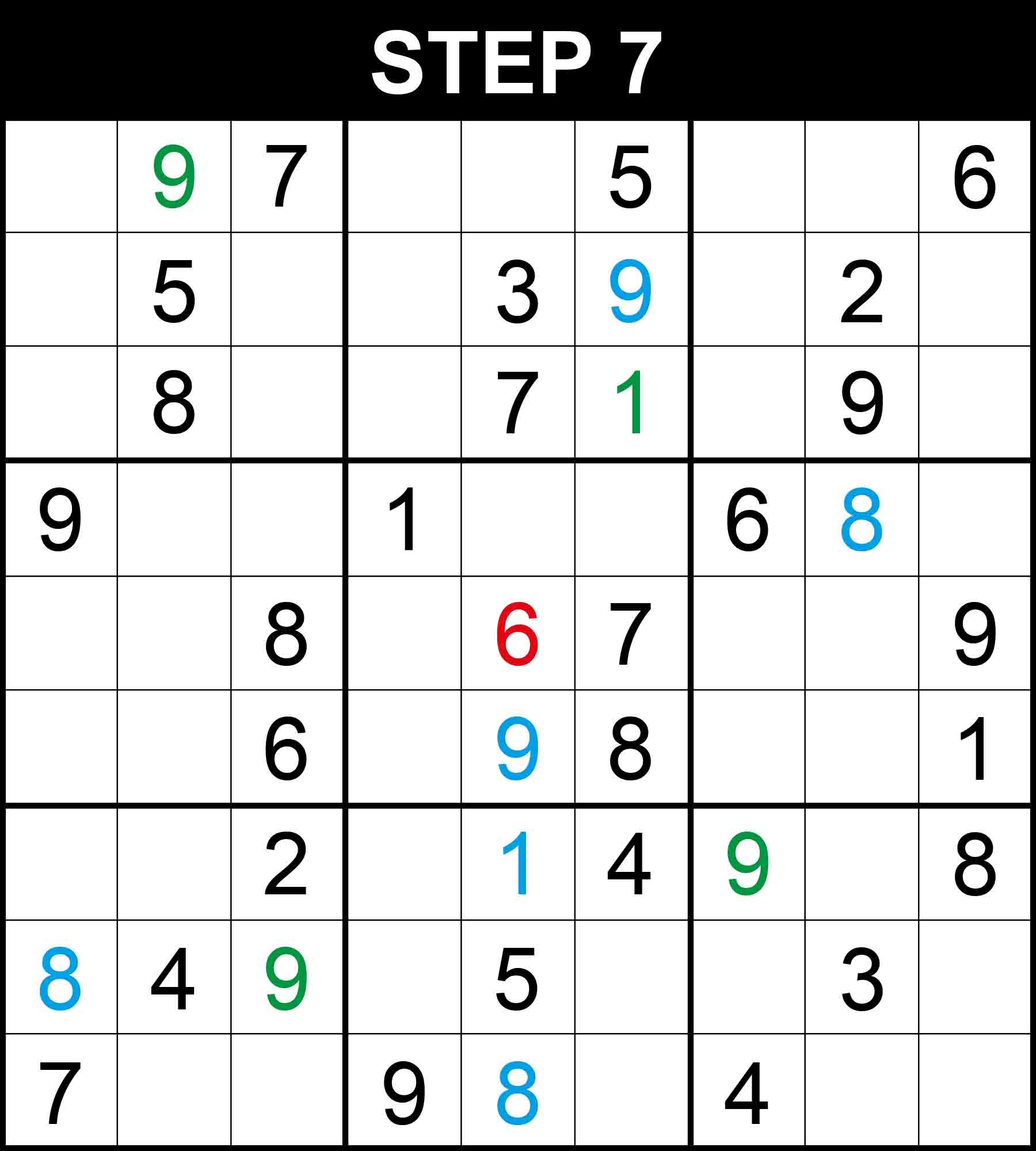
There is a single position for 1 in column 6. The other cells in this dimension cannot contain 1 because their rows, columns, or boxes already contain 1.
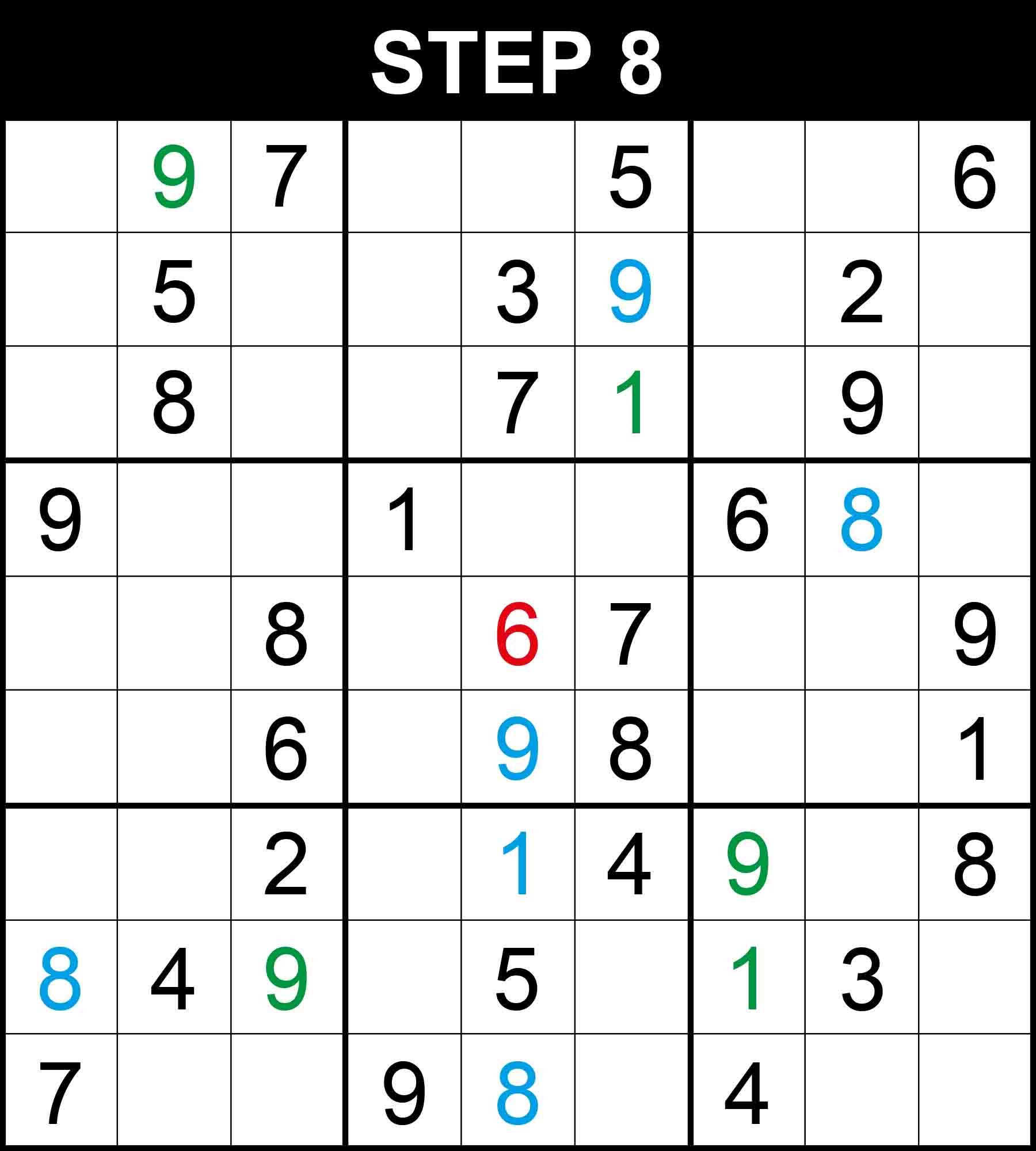
There is a single position for 1 in row 8. The other cells in this dimension cannot contain 1 because their rows, columns, or boxes already contain 1.
There is a single position for 1 in column 8. The other cells in this dimension cannot contain 1 because their rows, columns, or boxes already contain 1.
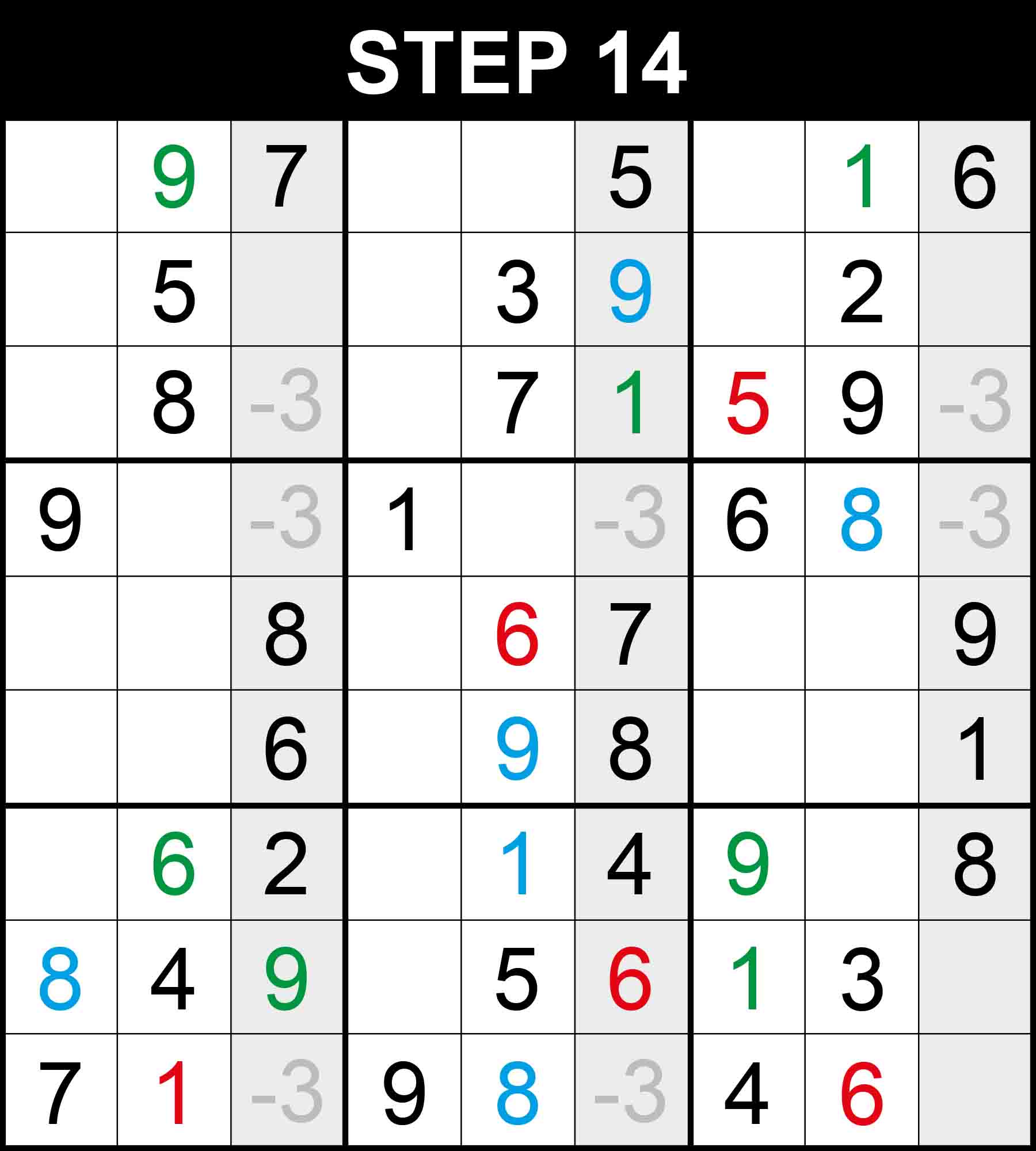
Looking at column 4, 6 is in one of two cells in box (1,2) and points vertically, thus eliminating one position for 6 at (8,4) in row 8. Therefore, There is a single position left for 6 in row 8 at (8,6).
Looking at columns 3, 6, and 9, the value 3 is restricted exactly to three rows 3, 4, and 9. Therefore each of those three rows contain a 3 that is restricted only to columns 3, 6, and 9. Therefore 3 can be eliminated from cell (3,8). 5 is the only missing value at (3,8).
Looking at columns 3, and 9, the value 5 is restricted exactly to two rows 4 or 9. Therefore each of those two rows contain a 5 that is restricted only to columns 3 and 9. Therefore 5 can be eliminated from cell (9,8). 6 is the only missing value at (9,8).
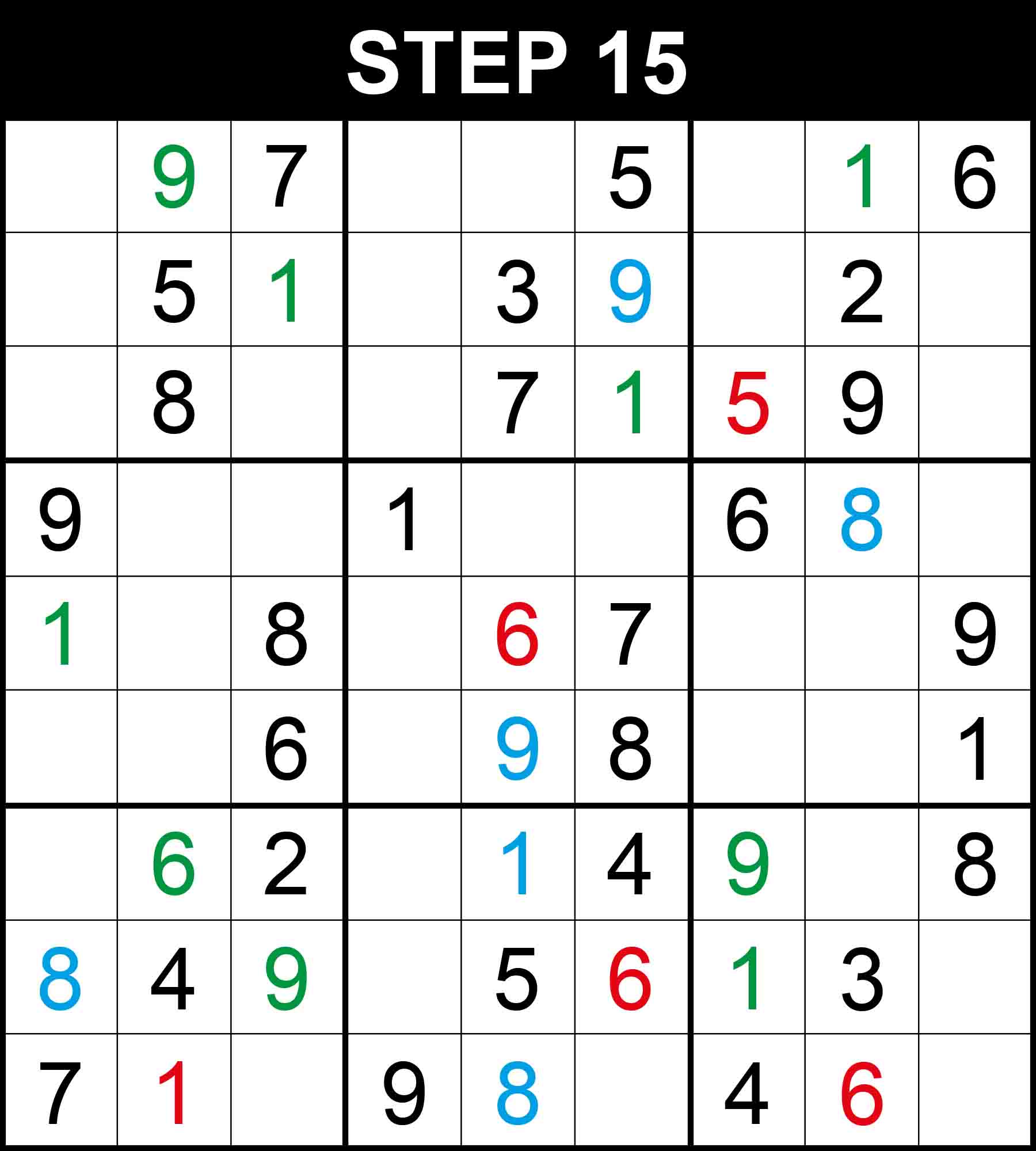
There is a single position for 6 in column 2. The other cells in this dimension cannot contain 6 because their rows, columns, or boxes already contain 6.
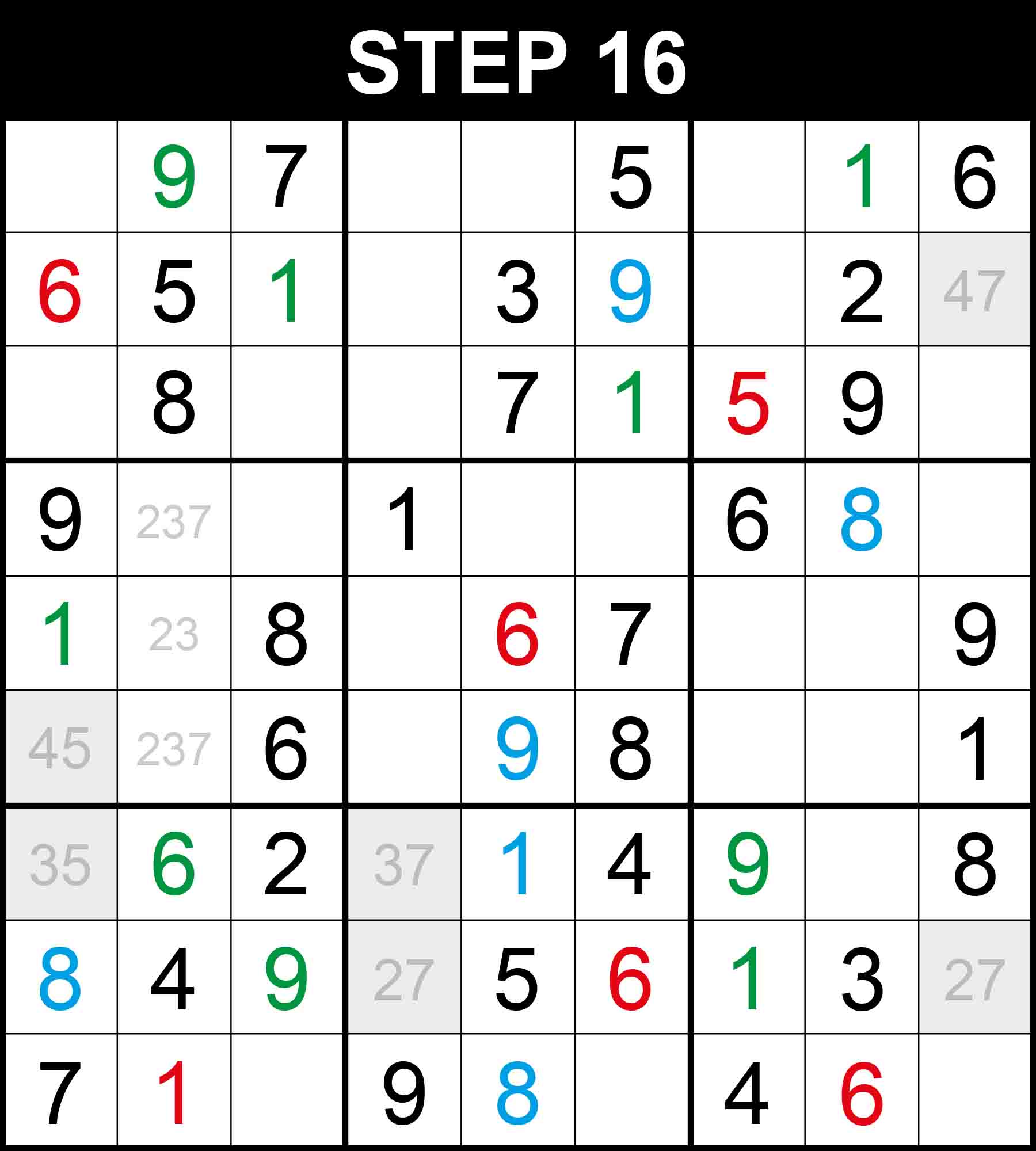
Looking at columns 3, 6, and 9, the value 3 is restricted exactly to three rows 3, 4, and 9. Therefore each of those three rows contain a 3 that is restricted only to columns 3, 6, and 9. Therefore 3 can be eliminated from cell (9,2). 1 is the only missing value at (9,2).
There is a single position for 1 in row 5, and 1 in column 3. The other cells in these dimensions cannot contain them because their rows, columns, or boxes already contain them.
Looking at cell (6,1) and cell (2,9), if the value in one of the two cells is not 4 then the value in the other has to be 4. Therefore, cell (2,1) cannot contain 4 and 6 is the only missing value at (2,1).
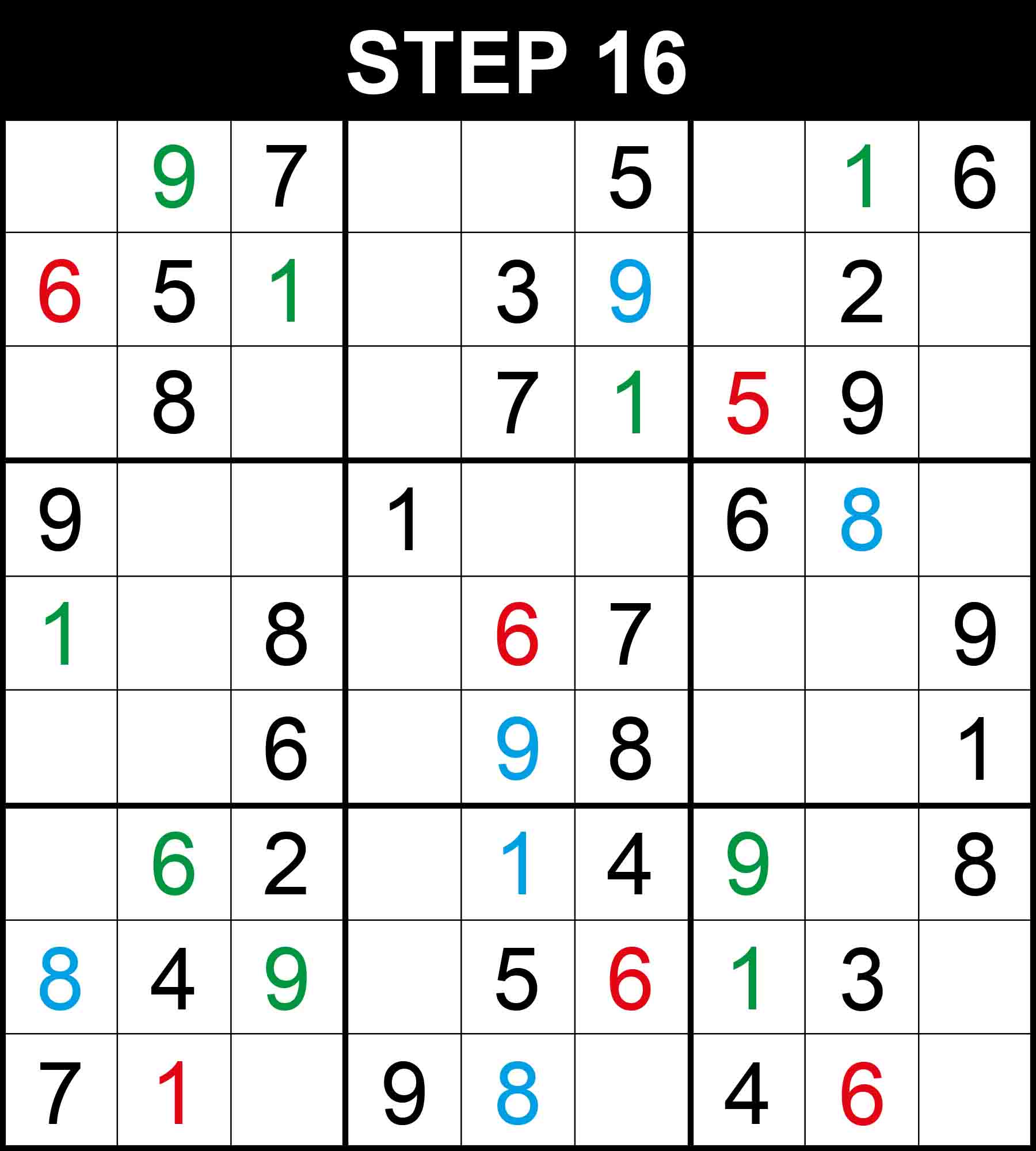
There is a single position for 6 in row 3. The other cells in this dimension cannot contain 6 because their rows, columns, or boxes already contain 6.
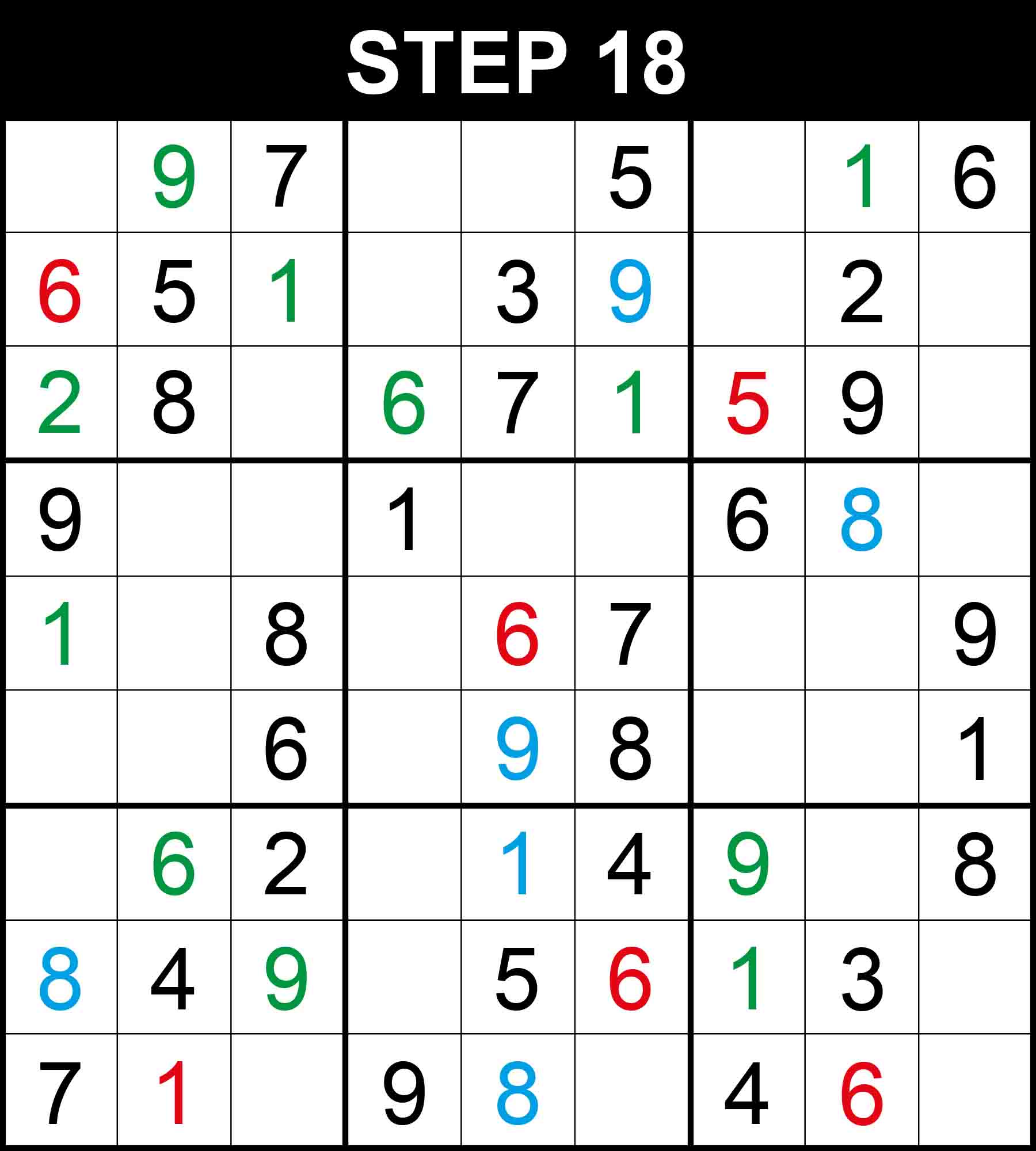
There is a single position for 2 in row 3. The other cells in this dimension cannot contain 2 because their rows, columns, or boxes already contain 2.
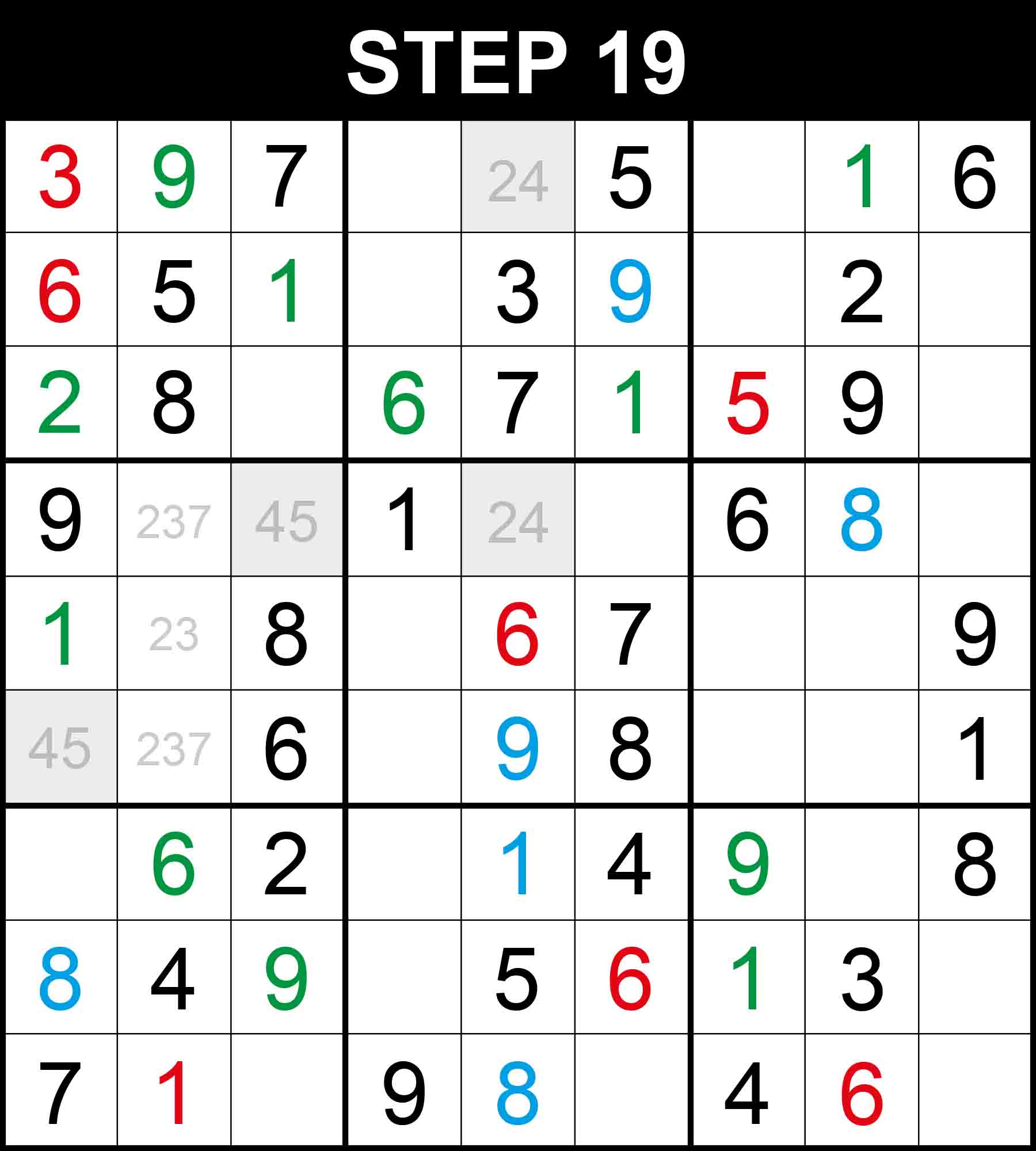
Looking at cell (6,1) and cell (1,5), if the value in one of the two cells is not 4 then the value in the other has to be 4. Therefore, cell (1,1) cannot contain 4 and 3 is the only missing value at (1,1).
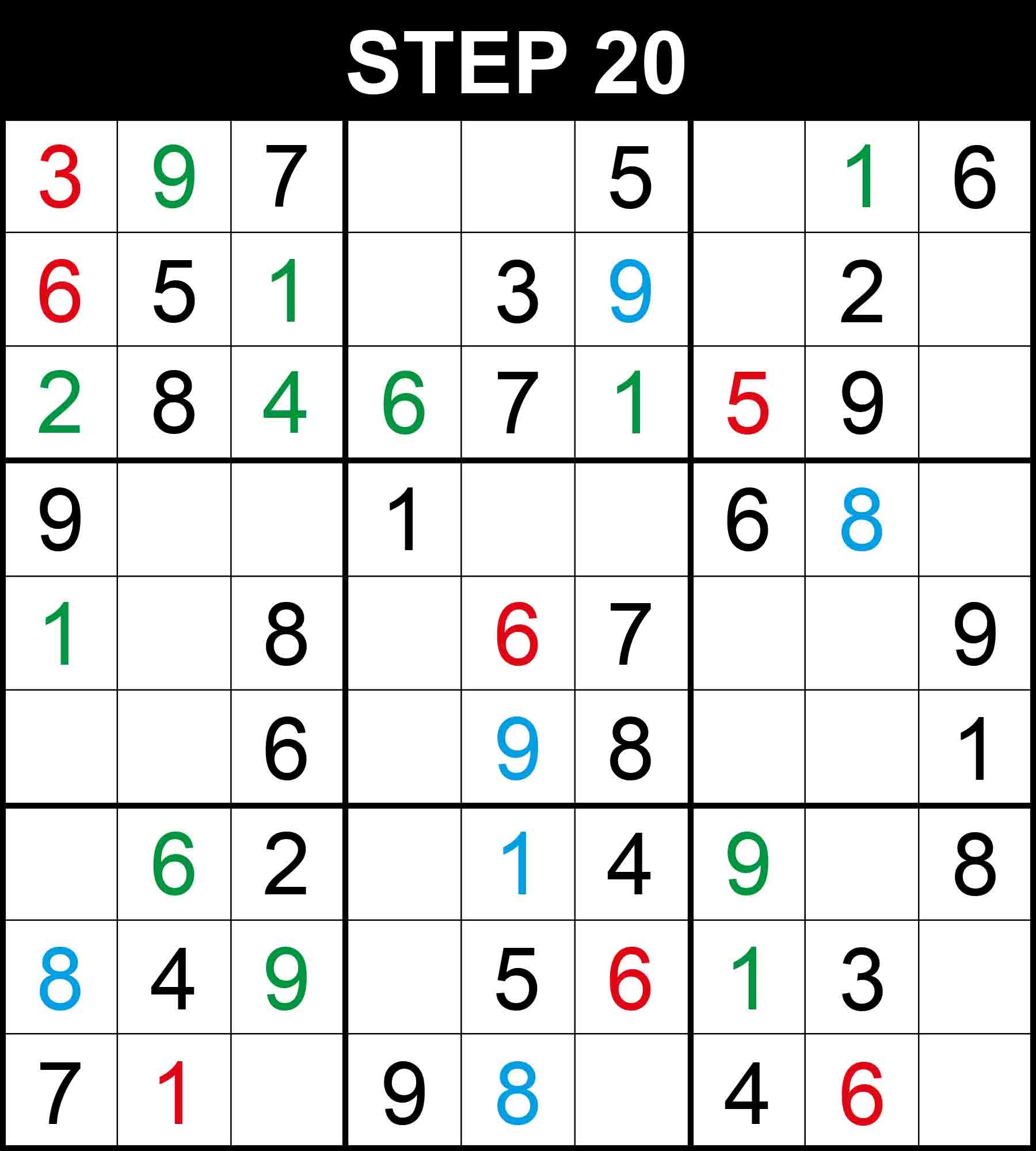
Looking at box (1,1), 4 is the only missing value at (3,3).
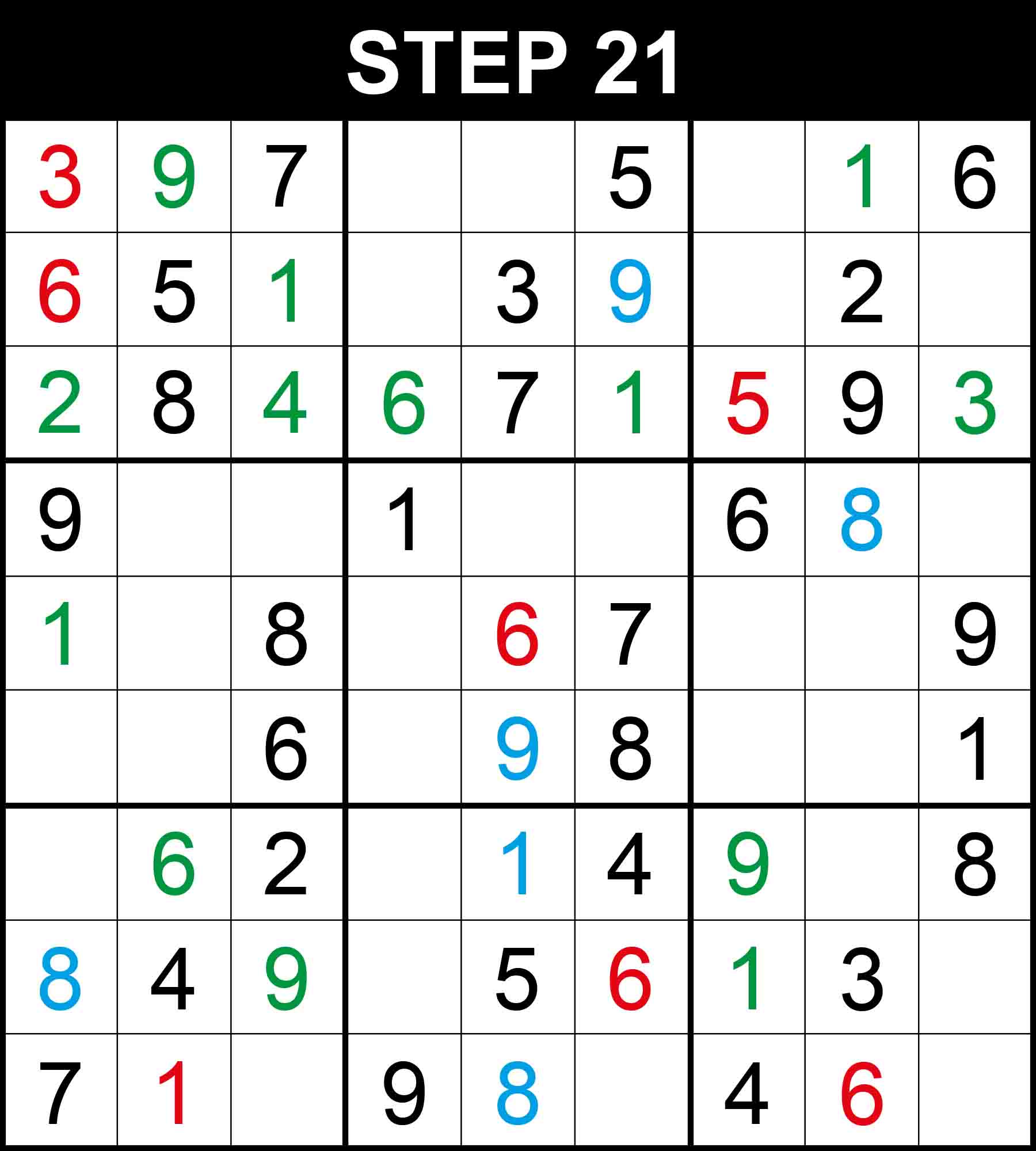
Looking at row 3, 3 is the only missing value at (3,9).
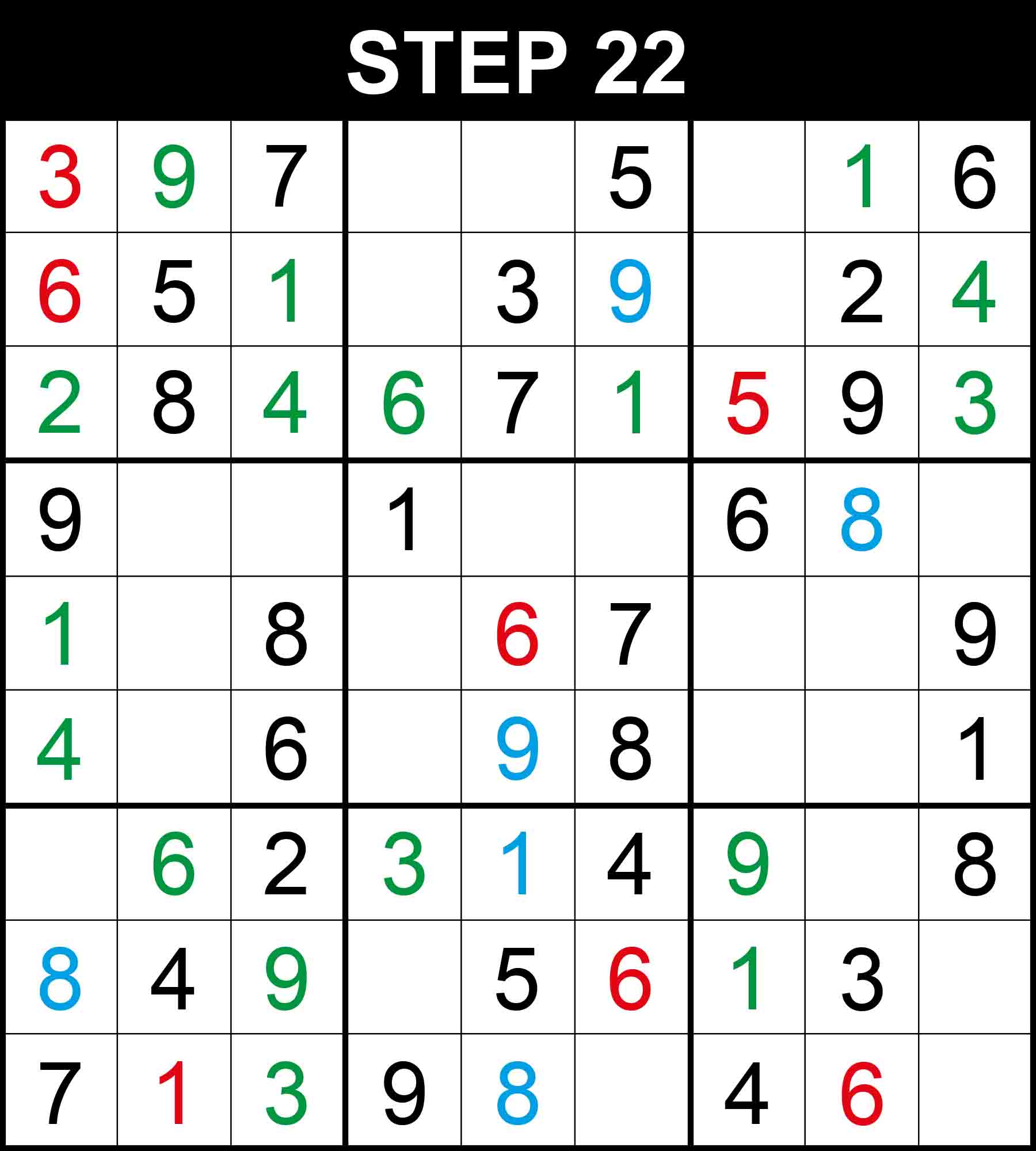
There is a single position for 3 in row 7, 4 in column 1, 4 in box (1,3), and 3 in box (1,3). The other cells in these dimensions cannot contain them because their rows, columns, or boxes already contain them.
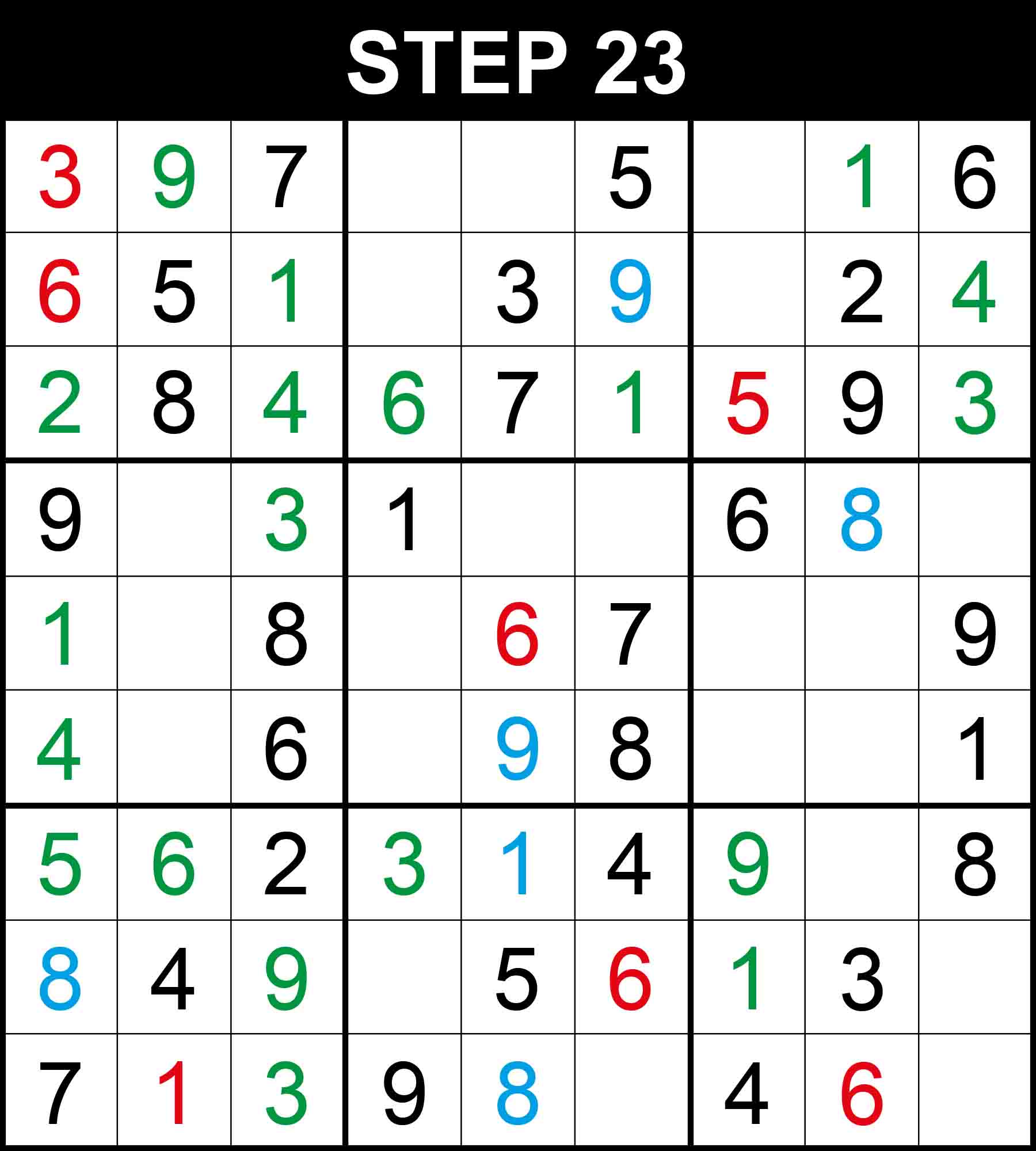
Looking at column 1, 5 is the only missing value at (7,1). Looking at column 3, 5 is the only missing value at (4,3).
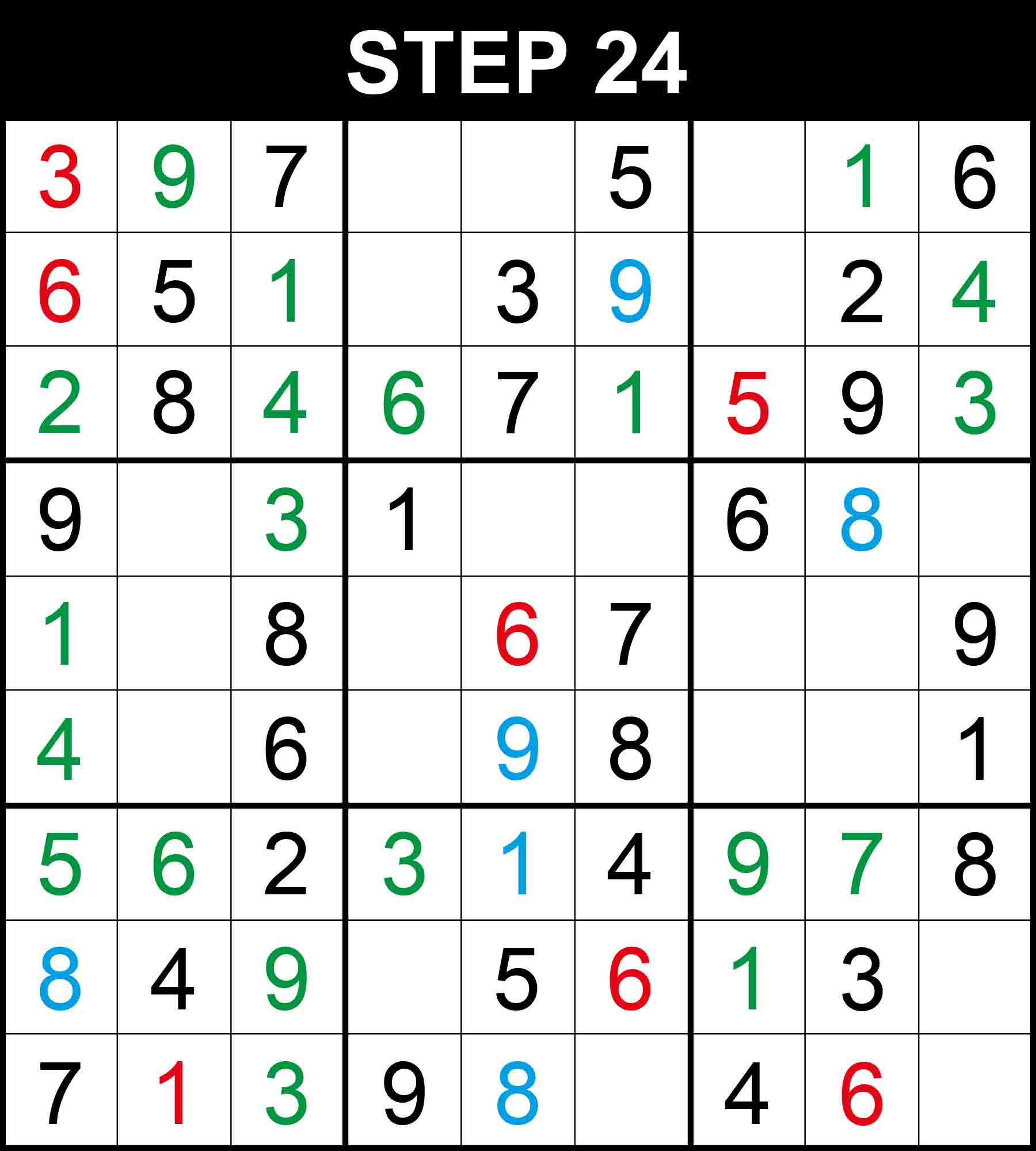
Looking at row 7, 7 is the only missing value at (7,8).
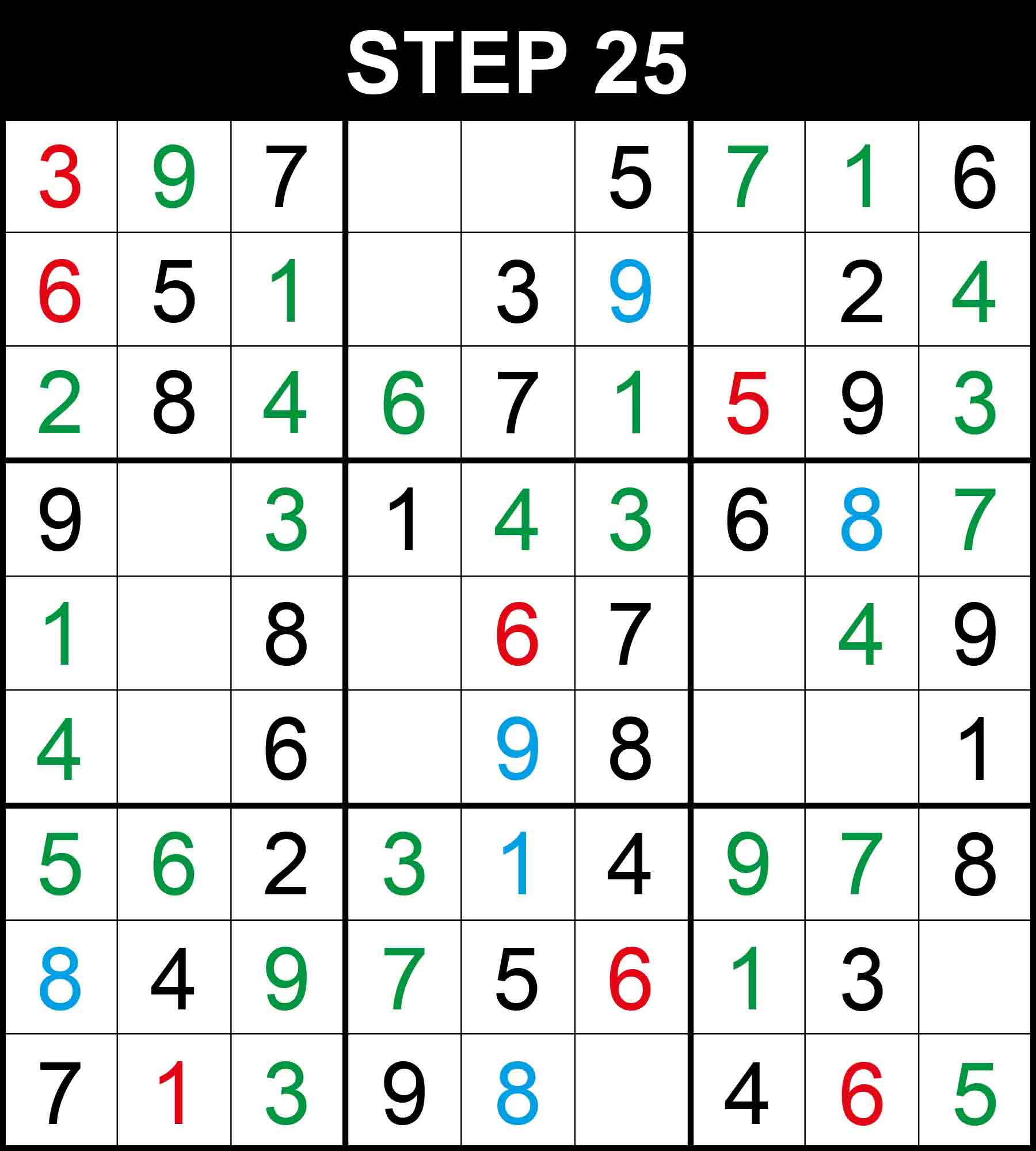
There is a single position for 7 in row 2, 4 in row 4, 7 in row 8, 5 in row 9, 3 in column 6, 4 in row 8, and 7 in column 9. The other cells in these dimensions cannot contain them because their rows, columns, or boxes already contain them.
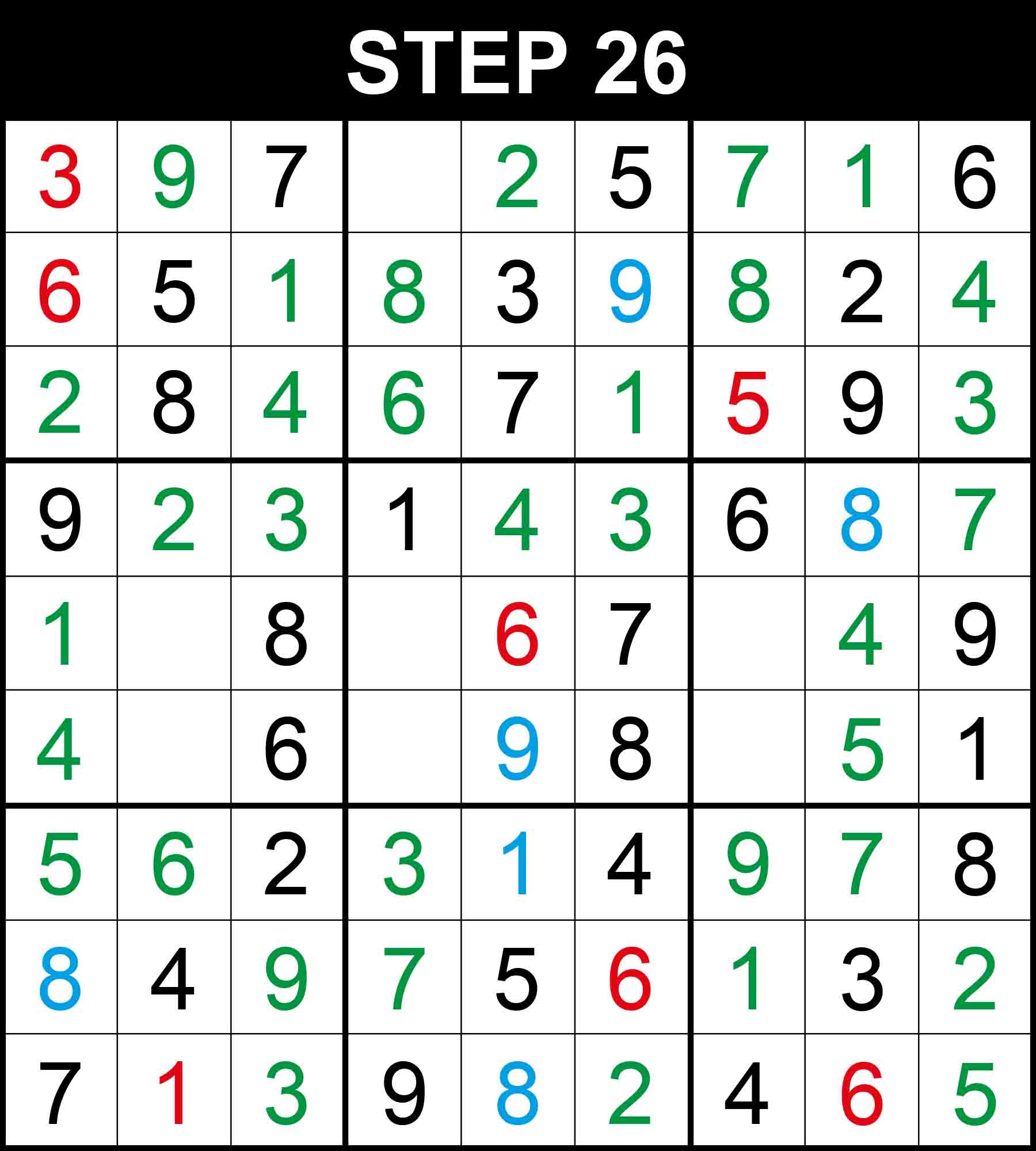
Looking at row 2, 8 is the only missing value at (2,4). Looking at row 4, 2 is the only missing value at (4,2). Looking at row 8, 2 is the only missing value at (8,9). Looking at row 9, 2 is the only missing value at (9,6). Looking at column 5, 2 is the only missing value at (1,5). Looking at column 8, 5 is the only missing value at (6,8). Looking at box (1,3), 8 is the only missing value at (1,7).
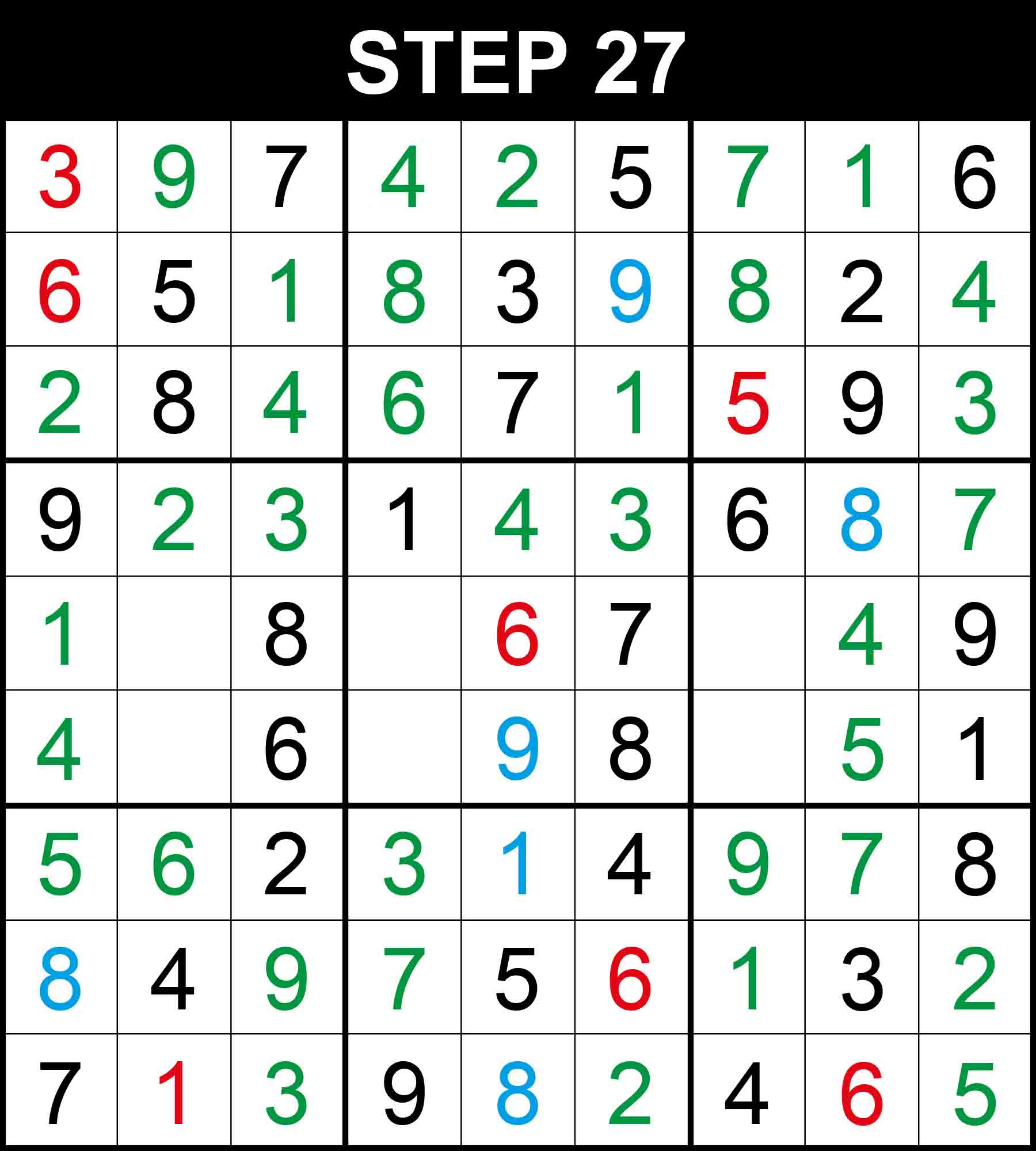
Looking at row 1, 4 is the only missing value at (1,4).
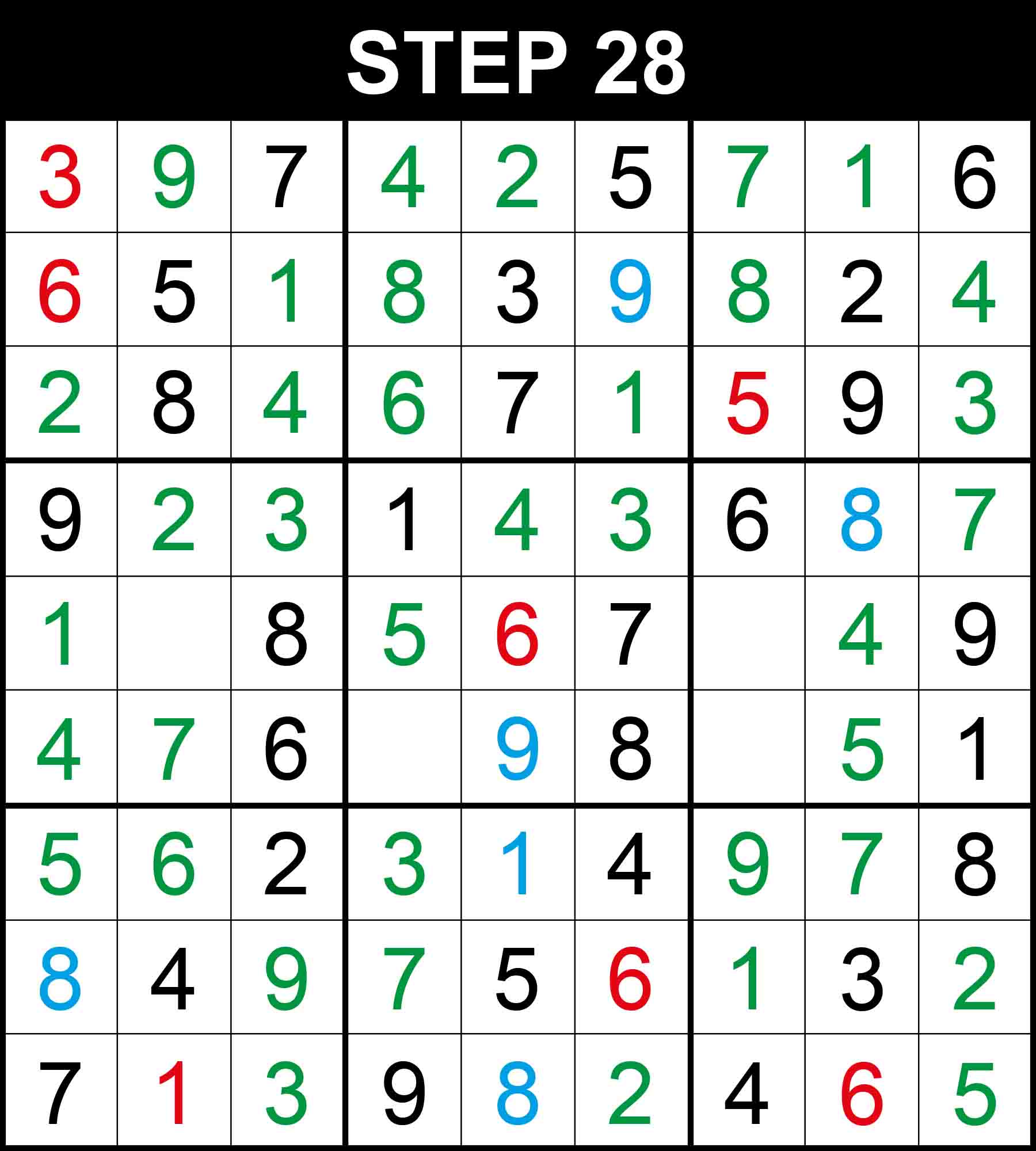
There is a single position for 5 in row 5, and 7 in row 6. The other cells in these dimensions cannot contain them because their rows, columns, or boxes already contain them.
Looking at column 2, 3 is the only missing value at (5,2). Looking at column 4, 2 is the only missing value at (6,4).
Looking at row 5, 2 is the only missing value at (5,7). Looking at row 6, 3 is the only missing value at (6,7).